Question

What is the shortest distance of the point (0,c) from the parabola $y={{x}^{2}}$ where $0\le c\le 5$.
(a) $c\,if\,0\le c\le \dfrac{1}{2}$
(b) $c\,if\,3\le c\le 5$
(c) $\sqrt{c-\dfrac{1}{4}}\,if\,\dfrac{1}{2}\le c\le 5,\,c\,if\,0\le c\le \dfrac{1}{2}$
(d) $\sqrt{c}$

Answer 1

Hint: In this question, we will write equation of shortest distance using distance formula, which is given as : the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $D=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$. Then we will minimise it using the concept of application of differentiation.

Complete step-by-step answer:
In the given question, we have parabola, $y={{x}^{2}}$.
We are to find the shortest distance of point (0.c) from parabola, where $0\le c\le 5$.
Let us consider the point, where the line segment of shortest distance from (o,c) meets parabola to be (a,b).
Let the shortest distance be D. The diagrammatic representation can be given as:

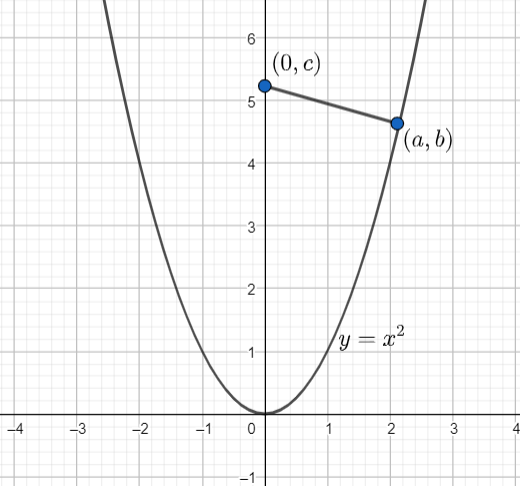
We know, the distance between the points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given as $D=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$ .
Thus, using the formula of distance between two point, we can write,
$\begin{aligned} & D=\sqrt{{{\left( a-0 \right)}^{2}}+{{\left( b-c \right)}^{2}}} \\\ & \Rightarrow D=\sqrt{{{a}^{2}}+{{\left( b-c \right)}^{2}}}.............(i) \\\ \end{aligned}$
Since, point (a,b) lies on the parabola, it will satisfy the equation of parabola. Therefore,
$b={{a}^{2}}$
Using this value of b in (i), we get,
$D=\sqrt{{{a}^{2}}+{{\left( {{a}^{2}}-c \right)}^{2}}}$
Squaring this equation on both sides, we get,
${{D}^{2}}={{a}^{2}}+{{\left( {{a}^{2}}-c \right)}^{2}}$
$\Rightarrow {{D}^{2}}={{a}^{2}}+{{\left( {{a}^{2}} \right)}^{2}}-2{{a}^{2}}.c+{{c}^{2}}$
$\Rightarrow {{D}^{2}}={{a}^{2}}+{{a}^{4}}-2{{a}^{2}}c+{{c}^{2}}$
$\Rightarrow {{D}^{2}}={{a}^{4}}+{{a}^{2}}\left( 1-2c \right)+{{c}^{2}}...........(ii)$
For the shortest distance, we need to minimise d. For which, we first need to find the critical point of equation (ii). Let us differentiate D with respect to a, so we get,
$2D\dfrac{dD}{da}=4{{a}^{3}}+2a\left( 1-2c \right)$
$\Rightarrow \dfrac{dD}{da}=\dfrac{4{{a}^{3}}+2a\left( 1-2c \right)}{2D}............(iii)$
To find critical point, we equate $\dfrac{dD}{da}$ with 0, so we get,
$\dfrac{dD}{da}=0$
$\Rightarrow \dfrac{4{{a}^{3}}+2a\left( 1-2c \right)}{2D}=0$
Multiplying 2D on both sides of the equation, we get,
$\begin{aligned} & 4{{a}^{3}}+2a\left( 1-2c \right)=0 \\\ & \Rightarrow 2a\left( 2{{a}^{2}}+1-2c \right)=0 \\\ \end{aligned}$
Therefore, either 2a = 0 or ${{a}^{2}}+1-2c=0$
$\Rightarrow a=0\,\,\,\,\,\,\,or\,\,\,\,\,\,2{{a}^{2}}=2c-1$
Taking root, we get,
$a=0\,\,\,\,or\,\,\,a=\pm \sqrt{\dfrac{2c-1}{2}}$
Here, for $\,0\le c\le \dfrac{1}{2}$ value under root of $a=\pm \sqrt{\dfrac{2c-1}{2}}$ will be negative, which will make a imaginary.
Therefore a=0. Now, double differentiating D, from equation (iii), we get,
$2{{\left( \dfrac{dD}{Da} \right)}^{2}}+2\dfrac{{{d}^{2}}D}{d{{a}^{2}}}=12{{a}^{2}}+2\left( 1-2c \right)$
For, $\,0\le c\le \dfrac{1}{2}$ and a=0.
$\dfrac{{{d}^{2}}D}{d{{a}^{2}}}$ will be positive.
Hence, a is a point of minima for D.
$b={{a}^{2}}={{0}^{2}}=0$
Hence the point on parabola of shortest distance from (0,c) is (0,0), when $\,0\le c\le \dfrac{1}{2}$.
$D=\sqrt{{{0}^{2}}+{{c}^{2}}}$
$=c$, When $\,0\le c\le \dfrac{1}{2}$
Now, when $\,\dfrac{1}{2}\le c\le 5$, for a=0 $\dfrac{{{d}^{2}}D}{d{{a}^{2}}}$ will be negative, hence not a point of minima.
But, for $\,\dfrac{1}{2}\le c\le 5$ and $a=\pm \sqrt{\dfrac{2c-1}{2}}$, $\dfrac{{{d}^{2}}D}{d{{a}^{2}}}$ will be positive, so it will be point of minima.
So, here $b={{a}^{2}}=\dfrac{2c-1}{2}$
So, point on parabola for shortest distance from (0,c) is $\left( \pm \sqrt{\dfrac{2c-1}{2}},\dfrac{2c-1}{2} \right)$ when $\,\dfrac{1}{2}\le c\le 5$.
So, here $D=\sqrt{{{a}^{4}}+{{a}^{2}}\left( 1-2c \right)+{{c}^{2}}}$
$=\sqrt{{{\left( \dfrac{2c-1}{2} \right)}^{2}}+\dfrac{2c-1}{2}\left( 1-2c \right)+{{c}^{2}}}$
$=\sqrt{\dfrac{4{{c}^{2}}-4c+1}{4}+\dfrac{\left( 2c-1 \right)\left( 1-2c \right)}{2}+{{c}^{2}}}$
Taking LCM and solving, we get,
$D=\sqrt{\dfrac{4{{c}^{2}}-4c+1+4c-8c-2+4c+4{{c}^{2}}}{4}}$
$=\sqrt{\dfrac{4c-1}{4}}=\sqrt{c-\dfrac{1}{4}}$
Hence, shortest distance is $\sqrt{c-\dfrac{1}{4}}$ if $\,\dfrac{1}{2}\le c\le 5$ and c is $\,0\le c\le \dfrac{1}{2}$.
Therefore, (c) is the correct option.

Note: While doing calculations, take care of the signs. Sign mistakes are very common and students can end up in getting the wrong answer. So, students should be very careful and should avoid sign mistakes.