Question

What is the shape of the graph ${{r}^{2}}=-\cos \theta$?

Answer 1

For solving this question you should know about the graph of $-\cos \theta$ and the range of this graph. And in this question if we find the range of $-\cos \theta$ then it will be $\dfrac{\pi }{2}$ to $\dfrac{3\pi }{2}$. And if we plot the graph for this then it becomes a loop and the reason for the loop is because the values of $-\cos \theta$ will always vary within the range of -1 to 1. And thus we get a looped shape for this.

Complete step by step answer:
According to our question we have to find the shape of the graph of ${{r}^{2}}=-\cos \theta$.
If we want to make a graph for ${{r}^{2}}=-\cos \theta$, then first we will find the range of $-\cos \theta$.
If we see the graph of $\cos \theta$, then:

So, the range of cosine function is -1 to 1.
If we see to $-\cos \theta$ then the range of $-\cos \theta$ is $-1\le -\cos \theta \le 1$ and the domain is \left( -\infty ,\infty \right),\left\\{ \theta |\theta \in R \right\\}.
So, the graph of $-\cos \theta$ is:

As per question ${{r}^{2}}=-\cos \theta$, so the shape will be symmetrical about the initial line and ${{r}^{2}}=-\cos \theta \ge 0,\theta \in \left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$, where $\cos \theta \le 0$.
So, here if we see the value of $-\cos \theta$ at different angles then:
At $\dfrac{\pi }{2}:-\cos \theta =0;\left( 0,\dfrac{\pi }{2} \right)$
At $\dfrac{2\pi }{3}:-\cos \theta =\dfrac{1}{\sqrt{2}}:\left( \dfrac{1}{\sqrt{2}},\dfrac{2\pi }{3} \right)$
At $\dfrac{3\pi }{4}:-\cos \theta =\dfrac{1}{\sqrt{\sqrt{2}}};\left( \dfrac{1}{\sqrt{\sqrt{2}}},\dfrac{3\pi }{4} \right)$
At $\dfrac{5\pi }{6}:-\cos \theta =\sqrt{\dfrac{\sqrt{3}}{2}};\left( \sqrt{\dfrac{\sqrt{3}}{2}},\dfrac{5\pi }{6} \right)$
At $\pi :-\cos \theta =1;\left( 1,\pi \right)$
Symmetry about the axis $\theta =\pi$ will be used to draw the other half of the loop.
We considered only $r=\sqrt{-\cos \theta }\ge \theta$ for making the loop we did not consider the non – positive $r=\sqrt{-\cos \theta }\le \theta$, for the opposite loop, for the same $\theta \in \left( \dfrac{\pi }{2},\dfrac{3\pi }{2} \right)$.
So, here the r is a single values function of $\theta$.

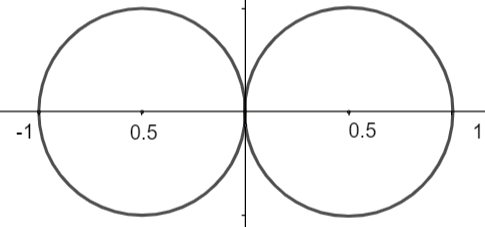
So, the shape of ${{r}^{2}}=\left( -\cos \theta \right)$ is a looped shape.

Note: While solving this question you should be careful about the domain and the range of the given function because only these both will decide the graph of a function. And it will provide the shape. And the graph for every function is different from each other, so always draw a fresh new graph.