Question

What is the shape of $S{{F}_{4}}$ (including bond angles)?

Answer 1

The shape of a molecule can be determined using the VSEPR model. The valence shell electron pair repulsion theory states that the molecules around the central atom will arrange in such a way that there is minimum repulsion between valence electron pairs of the atom.

Complete answer:
The VSEPR model of arrangement helps in increasing the stability of the molecule and decreasing its energy.
The repulsion between the electron pair increases in the following order
bp-bp < bp-lp < lp-lp
Now, the formula $A{{X}_{n}}{{E}_{m}}$ can be used while applying the VSEPR theory to represent the number of electron pairs around a central atom.
Where A represents the central atom, X represents the ligand bonded to the central atom, subscript n represents the number of ligands, E represents the lone pairs, and subscript m represents the number of lone pairs.
Now, the molecular geometry of the compound according to the $A{{X}_{n}}{{E}_{m}}$ formula are

$A{{X}_{n}}{{E}_{m}}$	MOLECULAR GEOMETRY
$A{{X}_{2}}{{E}_{0}}$	Linear
$A{{X}_{3}}{{E}_{0}}$	Trigonal Planar
$A{{X}_{2}}{{E}_{1}}$	Bent
$A{{X}_{4}}{{E}_{0}}$	Tetrahedral
$A{{X}_{3}}{{E}_{1}}$	Trigonal Pyramidal
$A{{X}_{2}}{{E}_{2}}$	Bent
$A{{X}_{5}}{{E}_{0}}$	Trigonal Bipyramidal
$A{{X}_{4}}{{E}_{1}}$	Seesaw
$A{{X}_{3}}{{E}_{2}}$	T-Shaped
$A{{X}_{2}}{{E}_{3}}$	Linear

Now, in $S{{F}_{4}}$, the valency of sulfur atoms is 6. Since it is single-bonded with 4 fluorine atoms, there is 1 lone pair.
Hence it is of the molecule type $A{{X}_{4}}{{E}_{1}}$ and has a see-saw shape where all bond angles are different and as follows.

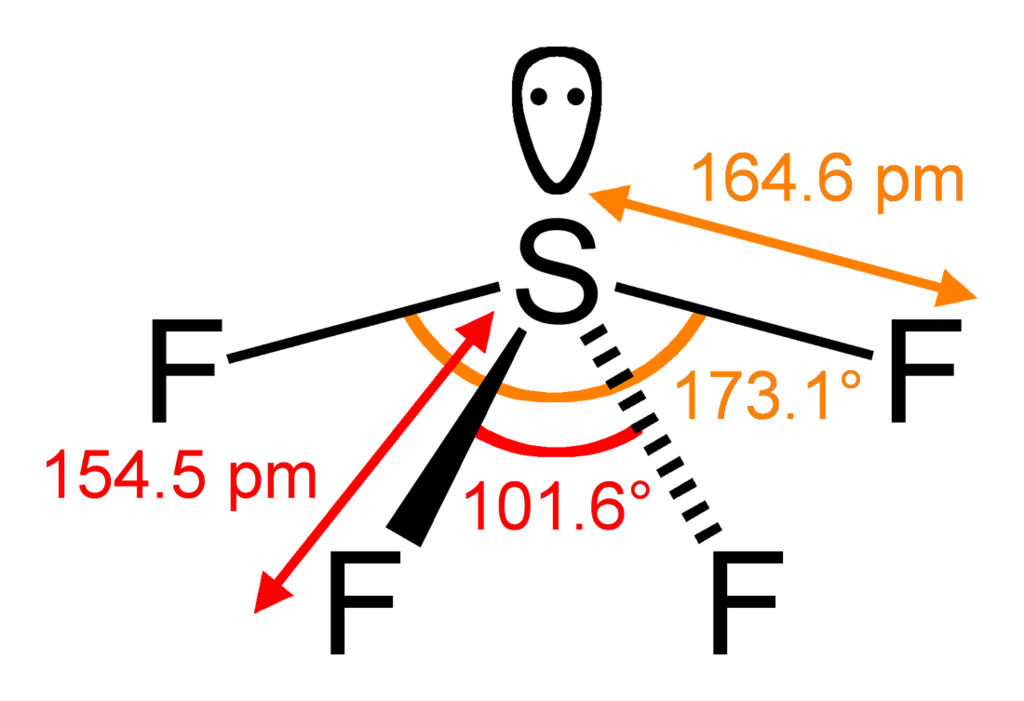
Note:
It should be noted that the sum of the coordination number of the central atom (number of atoms bonded to the central atom) and the number of valence electron lone pairs on the central atom gives the steric number of the compound.
Steric Number = n + m
For $S{{F}_{4}}$, n = 4 and m = 1.
So, the steric number is 5.