Question

What is the shape of d-orbital?
A.Spherical
B.Dumb bell
C.Double-dumb bell
D.No definite shape

Answer 1

In atomic theory and quantum mechanics, an atomic orbital is defined as a mathematical function which describes the location and wave-like behaviour of an electron.
These mathematical functions can be used to calculate the probability of finding any electron of an atom in a particular region around the nucleus.
There are four types of atomic orbitals: s (sharp), p (principle), d (diffuse) and f (fundamental).

Complete step by step answer:
Now let us look into the d-orbitals:
The mathematical equation that is used to describe that particular orbital defines the shape of that orbital. d-orbitals have a shape called double dumb bell, as shown in the following diagram:

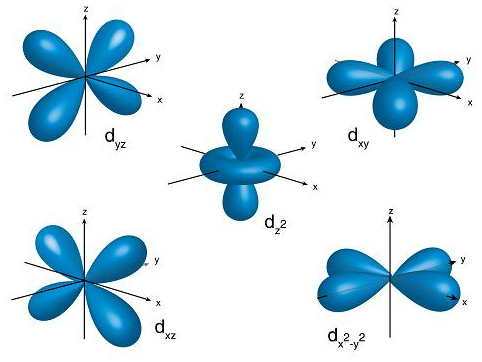
There are five types of d-orbitals namely, ${{\text{d}}_{{\text{xy}}}}$, ${{\text{d}}_{{\text{yz}}}}$, ${{\text{d}}_{{\text{xz}}}}$, ${{\text{d}}_{{{\text{x}}^{\text{2}}}{\text{ - }}{{\text{y}}^{\text{2}}}}}$ and ${{\text{d}}_{{{\text{z}}^{\text{2}}}}}$. Each of these have a capacity of 2 electrons each of opposite spin. Thus, d-orbital has a capacity of 10 electrons in total.
Hence, the correct option is C.

Note: Other orbitals are:
s-orbital: it is spherical and has a capacity of 2 electrons.
p-orbital: there are three types of p-orbitals, namely ${{\text{p}}_{\text{x}}}$, ${{\text{p}}_{\text{y}}}$ and ${{\text{p}}_{\text{z}}}$. Each of these has a capacity of 2 electrons and hence p-orbital has a capacity of 6 electrons in total. The shape of p-orbital is called a dumb bell.
d-orbital: discussed above
f-orbital: there are 7 f-orbitals, each having a capacity of 2 electrons so f-orbital has a capacity of 14 electrons in total. The shape of the f-orbital is fairly complicated and very hard to understand.
Please remember that orbitals are a mathematical expression. And are imaginary surfaces where the probability of finding an electron is nearly maximum.