Solveeit Logo
Login

Question

Question: What is the relationship between the rectangle form of complex numbers and their corresponding polar...

What is the relationship between the rectangle form of complex numbers and their corresponding polar form?

Explanation

Solution

To solve this kind of problem we need to know the concept of rectangular form and polar form of coordinates. The polar form is where a complex number is denoted by the length and the angle of its vector. In the case of Rectangular form a complex number is denoted by its respective horizontal and vertical components.

Complete step by step solution:
The question asks us to find the relation between the rectangular form of complex number and the polar form of complex number. To start with the definition of the rectangular form of complex number form of complex number which is written in the form of z=a+jbz=a+jb where a and b are the real numbers.
“a” and “b” are the coordinates of a point representing the complex number on a special plane called (Argand-Gauss) where on the x axis we have the real part (the number a) and on the y axis the imaginary (the b number, associated with j). The above explanation could be much understandable with the graph shown below:

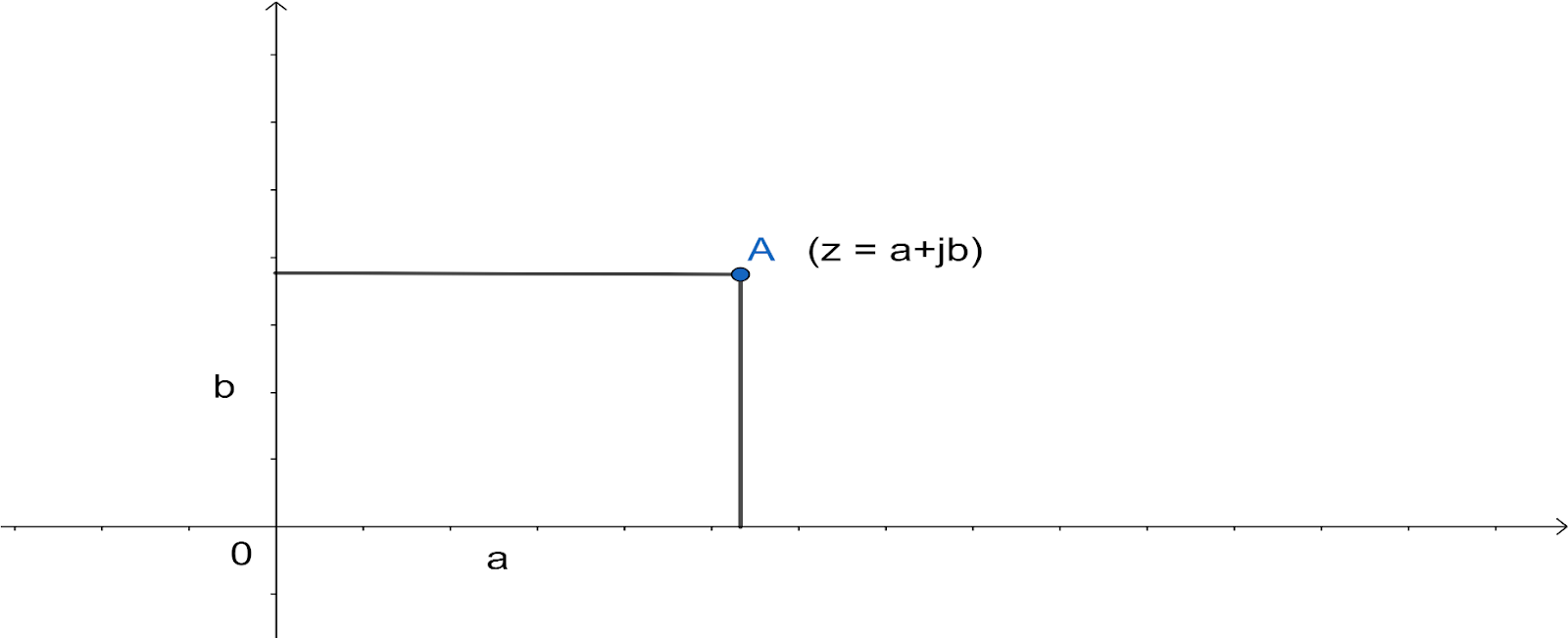
Taking the discussion towards the polar form of the coordinate for the given complex number. In the polar form for the representation of complex numbers the two independent variables are the magnitude rr and the argument α\alpha . Now here the argument α\alpha is basically the angle between the magnitude and x-axis while rr is the magnitude of the complex number. The above statement will be much clear with the below diagram:

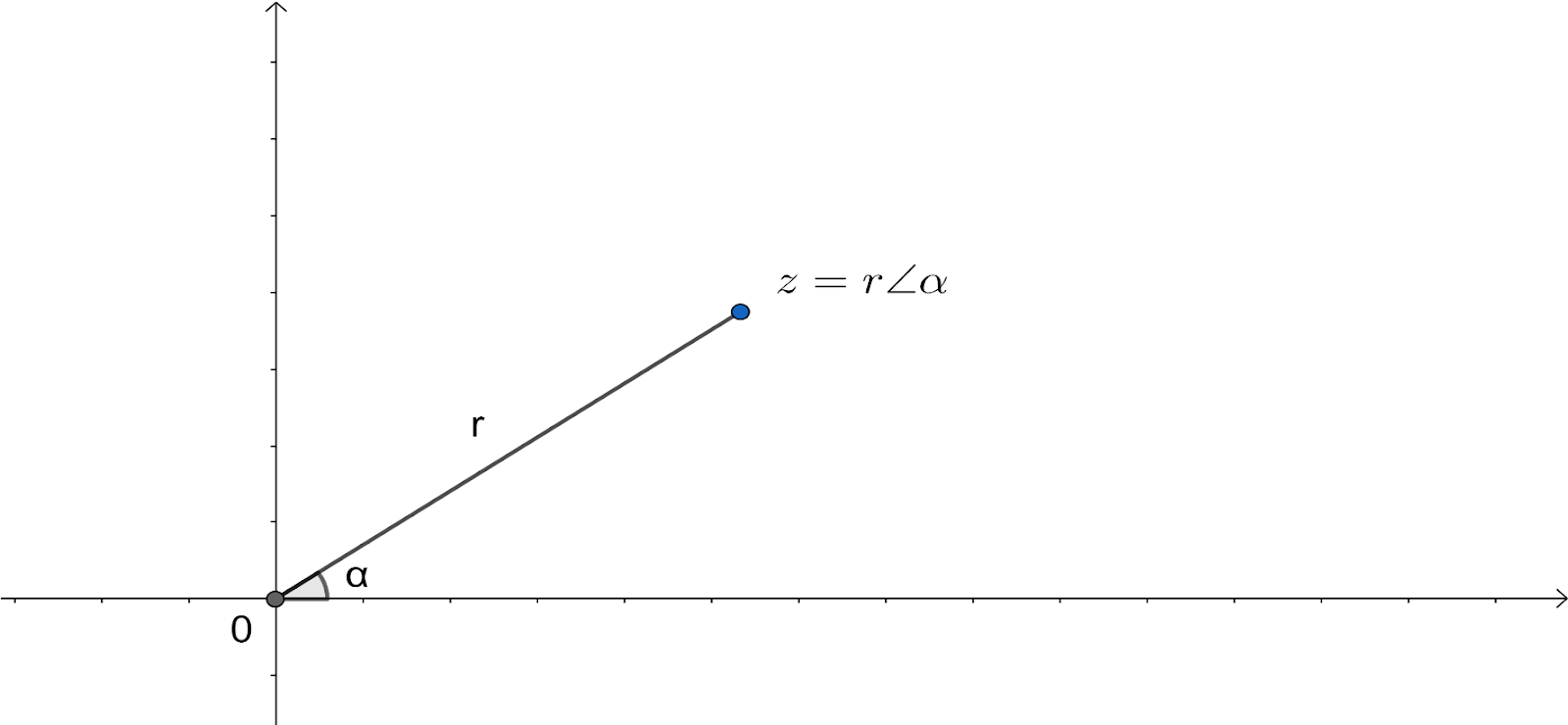
On combining the two coordinate system of the complex number, we get the following diagram of the representation of the complex number:


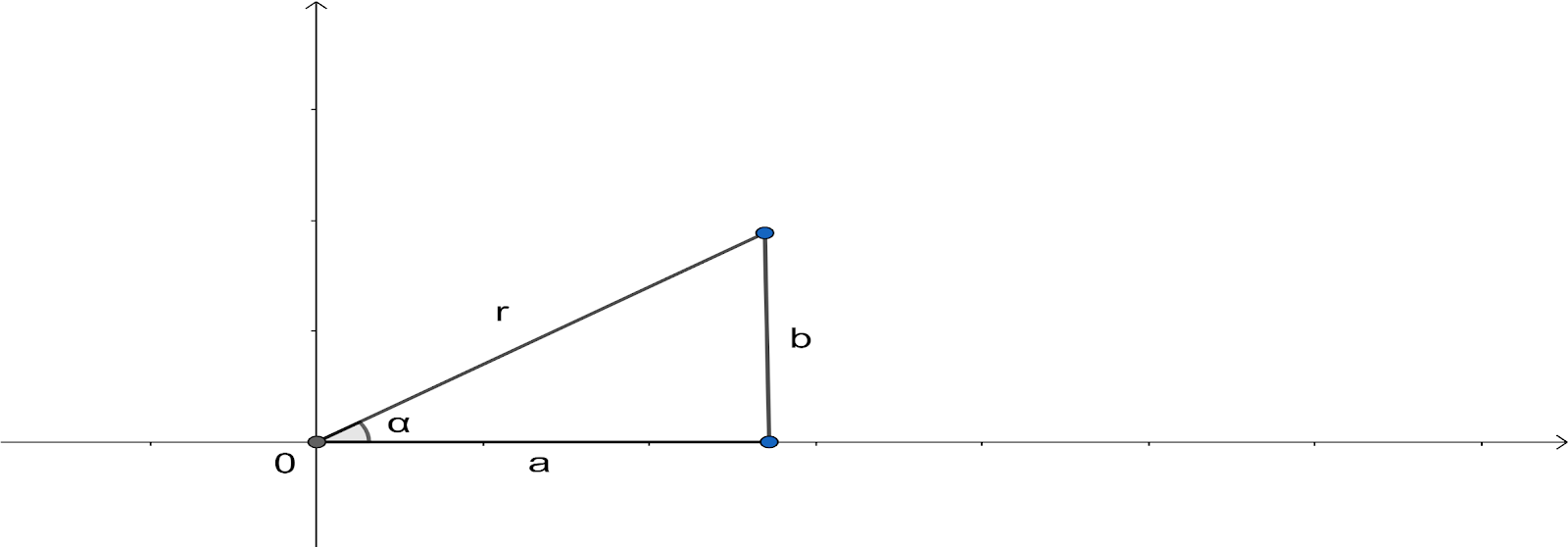
Some of the relationships between the two forms are:

  1. Pythagoras Theorem: which is used to link the length r with a and b r=a2+b2r=\sqrt{{{a}^{2}}+{{b}^{2}}} 2) Inverse trigonometric functions used to link the angle q with a and b q=arctan⁡(ba)q=\arctan \left( \dfrac{b}{a} \right)

Note: The arctangent of x is defined as the inverse tangent function of x when x is real. When the tangent of y is equal to x: tan y = x. Then the arctangent of x is equal to the inverse tangent function of x, which is equal to y: arctan !! !! x = tan−1 !! !! x = y\text{arctan }\\!\\!~\\!\\!\text{ x = ta}{{\text{n}}^{-1}}\text{ }\\!\\!~\\!\\!\text{ x = y}