Question

What is the relationship between the normal curve and the standard deviation?

Answer 1

In this problem, we can see the relationship between the normal curve and the standard deviation. We should know that the graph of the normal distribution depends upon two factors, the mean and the standard deviation, where the mean of the distribution determines the location of the centre of the graph and the standard deviation determines the height and the width of the graph. We can now see about them.

Complete step by step solution:
Here we can see the relationship between the normal curve and the standard deviation.
We should know that the graph of the normal distribution depends upon two factors, the mean and the standard deviation.
The normal distribution curve is the distribution of values around the mean of an evenly dispersed population, where standard deviation is the calculation of the width of that curve based on a sample or a population value. The normal curve is bell shaped and the normal curve is asymptotic to the base line.
The standard normal distribution is a normal distribution with mean, $\mu =0$ and the standard deviation,$\sigma =1$.

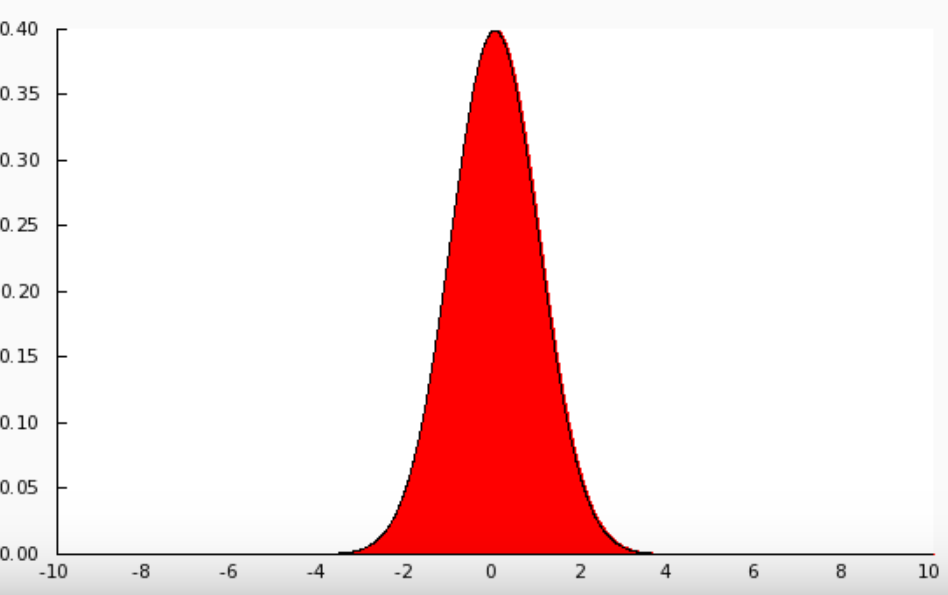
We can see the normal curve here.

Note: We should always remember the normal curve and the standard deviation. We should know that the graph of the normal distribution depends upon two factors, the mean and the standard deviation, where the mean of the distribution determines the location of the centre of the graph and the standard deviation determines the height and the width of the graph. The standard normal distribution is a normal distribution with mean, $\mu =0$ and the standard deviation,$\sigma =1$.