Question

What is the relationship between sine and cosine?

Answer 1

Here the given question is about the relationship between sine and cosine. Before starting this question, we need to know about what is the definition of sine and cosine. After that by illustrating some triangles we can find out the relationship between sine and cosine.

Complete step-by-step solution:

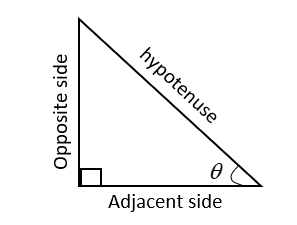
If we consider the above right-angled triangle, a right-angled triangle containing one of its angles is ${{90}^{\circ }}$,hypotenuse is the longest side, which is one opposite to the right angle. The adjacent side is the side which is between the angle to be determined and the right angle. From the figure,

& \text{sin}\theta \text{=}\dfrac{\text{opposite side}}{\text{hypotenuse}} \\\ & \text{cos}\theta \text{=}\dfrac{\text{adjacent side}}{\text{hypotenuse}} \\\ \end{aligned}$$ The sine is defined as it is the trigonometric function which is equal to the ratio of length of opposite side to the length of the hypotenuse. Similarly, the cosine is defined as it is the trigonometric function which is equal to ratio of the length of the adjacent side to the length of the hypotenuse. There are six basic trigonometric ratios for the right-angled triangle. They are sin, cos, tan, cosec, sec, cot which stands for Sine, Cosine, Cosecant, Tangent, Secant respectively. Sine and Cosine are basic trigonometric ratios which tells about the shape of the right triangle. Some basic relations between sine and cosine are $$\begin{aligned} & {{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta \\\ & {{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \\\ \end{aligned}$$ $$\begin{aligned} & \sin 2\theta =2\sin \theta \cos \theta \\\ & \cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \\\ \end{aligned}$$ If the angles in a right-angled triangle are acute angles, then $$\text{sin A=cos B}$$ If these acute angles of a right triangle measure to $${{90}^{\circ }}$$, then these acute angles are complementary. Then we can write as $$\begin{aligned} & \text{sin }\theta \text{=cos}\left( 90-\theta \right) \\\ & \text{cos }\theta \text{=sin}\left( 90-\theta \right) \\\ \end{aligned}$$ **Note:** Students do not understand how to approach a given trigonometric problem from the concept. Students make errors in applying identities and also do errors in calculations. Most students make errors at the manipulation of trig ratios using formulas. Understanding the trigonometric based question is also a time taking process.