Question

What is the relation between speeds of points $A$ and $B$ in the given figure?

(A) ${V_A} = {V_B}\cot \theta$
(B) ${V_A} = {V_B}\cos \theta$
(C) ${V_B} = {V_A}\cos \theta$
(D) ${V_B} = {V_A}\sec \theta$

Answer 1

Hint : As only the speed is to be found here, we will ignore the direction of velocity and the line of action of velocity. We only need to find the relation between the magnitudes of both velocities or say the relation between both speeds.

Complete Step By Step Answer:
Here, consider the figure as two strings are wrapped around the two pulleys. We are shown that the point $A$ moves downward.
This implies from the figure that the point $B$ should move upwards.
Hence, both velocities are opposite in direction. There might be a condition possible where both velocities cancel each other and there is no movement in the system.
Now, when the velocity is zero, it implies that the direction is opposite and the magnitude is the same.
The magnitude of velocity in the scalar factor is called speed.
Hence, we can say that the speed in both directions is the same.
But, from the geometry of the figure, we can understand that speed of $B$ is upwards, but not vertically upwards.
The movement of $B$ is along the string or wire. As there are two strings in different directions, the resultant speed might be upwards.
Let us consider only one side of the given arrangement as shown below,

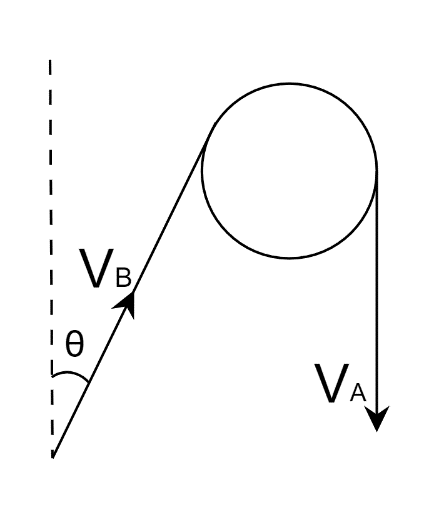
Here, we can see that speed of $A$ is vertically downwards and speed of $B$ is upwards at an angle of $\theta$ with the vertical.
The component of the speed of $B$ in the vertical direction, from the figure, is ${V_B}\cos \theta$
Thus, the derived relation is ${V_A} = {V_B}\cos \theta$
Thus, the correct answer is Option $(B)$ .

Note :
The point to note here is that we are only concerned with the magnitude of the velocity, we don’t need to find the directions of the velocity. Though here, we can say from the geometry of the figure that the speeds are in opposite directions.