Question

What is the reading of the voltmeter in the following figure?

Answer 1

Voltmeter is a device which is used to measure the potential difference across the two ends of a resistance, it is always connected parallel to the resistance across which potential difference or voltage difference is to be measured.
For equivalent resistance, formula to be used:
For resistances in parallel:$\dfrac{1}{{{R}_{eq}}}\,=\,\dfrac{1}{{{R}_{1}}}\,+\,\dfrac{1}{{{R}_{2}}}$
For resistances in series: ${{R}_{eq}}\,=\,{{R}_{1}}\,+\,{{R}_{2}}$
Also, in parallel combinations potential drop across the resistor will be equal.

Complete step by step solution:
Ideally the resistance of a voltmeter should be infinite so that no current should flow through it but practically it is not possible. In practical conditions some current flows through the voltmeter.
Let the current flowing in the circuit be $I$and the current flowing through the voltmeter be $i$.

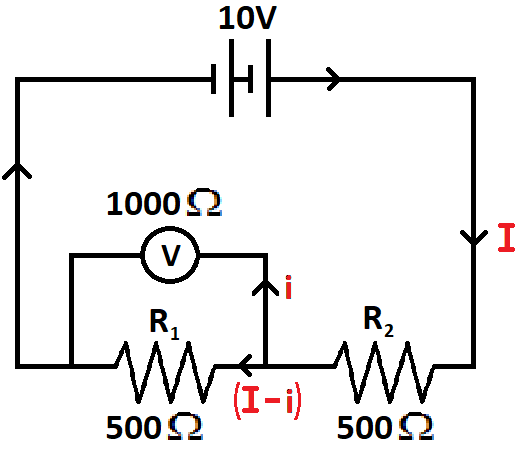
Here the voltmeter and the resistance ${{R}_{1}}$ is in parallel combination.
Total resistance for parallel combination: $\dfrac{1}{{{R}_{eq}}}\,=\,\dfrac{1}{{{R}_{1}}}\,+\,\dfrac{1}{{{R}_{2}}}$
$\Rightarrow \,\dfrac{1}{{{R}_{eq}}}\,=\,\dfrac{1}{500}\,+\,\dfrac{1}{1000}\,=\,\dfrac{2+1}{1000}\,=\,\dfrac{3}{1000}$
$\therefore \,{{R}_{eq}}\,=\,\dfrac{1000}{3}\,\Omega$
Now the equivalent resistance of Voltmeter and $500\,\Omega$(${{R}_{1}}$) is in series combination with $500\,\Omega$
Total resistance for series combination:${{R}_{eq}}\,=\,{{R}_{1}}\,+\,{{R}_{2}}$
$\Rightarrow \,{{R}_{eq}}\,=\,\dfrac{1000}{3}\Omega \,+\,500\Omega \,=\,\dfrac{2500}{3}\,\Omega$
Total current flowing in the circuit
$I\,=\,\dfrac{V}{{{R}_{total}}}\,=\,\dfrac{10\,V}{\dfrac{2500}{3}\Omega }\,=\,\dfrac{10\times 3}{2500}A\,=\,\dfrac{3}{250}A$
As the voltmeter and $500\,\Omega$ are in parallel and we know that in parallel combination the potential drop across resistances are equal.
Mathematically, ${{V}_{Voltmeter}}\,=\,{{V}_{500\Omega }}$
$\Rightarrow \,{{i}_{1}}\times {{R}_{1}}\,=\,{{i}_{2}}\times {{R}_{2}}$
$\Rightarrow \,500\times (I-i)\,=\,1000\times i$
$\Rightarrow \,(I-i)\,=\,2i$
$\Rightarrow \,i\,=\,\dfrac{I}{3}\,=\,\dfrac{3}{250}\times \dfrac{1}{3}A\,=\,\dfrac{1}{250}A$
Hence, Voltage across the voltmeter
${{V}_{Voltmeter}}\,=\,i\times \,{{R}_{Voltmeter}}$
${{V}_{Voltmeter}}\,=\,\dfrac{1}{250}\times 1000\,=\,4\,V$

Note:
As the voltmeter has very large resistance so it is not connected in series instead it is connected in parallel.
Practically voltmeter is not used in measuring potential difference across a resistor, because voltmeter has a finite resistance. (Ideally it should be $\infty$) in other words it draws some current from the circuit. To overcome this problem potentiometer is used because at the instant of measurement, it draws no current from the circuit. It means its effective resistance is infinite.