Question

What is the reading of the ammeter as per the figure shown?

(A) $\dfrac{1}{8}A$
(B) $\dfrac{3}{4}A$
(C) $\dfrac{1}{2}A$
(D) $2\;A$

Answer 1

Hint : Here, first we need to find the equivalent resistance of the given resistances by simplifying the circuit diagram and finding the series and parallel resistances. Then as per Ohm’s Law, by dividing the equivalent resistance by the cell voltage, we can get the ammeter reading.

Complete Step By Step Answer:
To begin let us rearrange the circuit diagram to get a better knowledge about the series and parallel arrangement of resistances as shown in the figure below

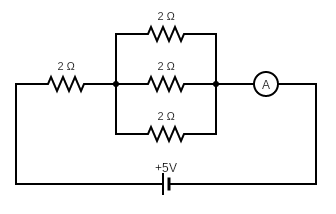
We can rearrange the parallel resistances in this way because from the given figure we can see that one end of all resistors is connected to the series resistance $2\Omega$ and another end is connected to the Ammeter
This rearrangement is correct as the cell is still between the series resistance $2\Omega$ and the ammeter.
For the parallel connection of resistors, the equivalent resistance can be found as
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}}$
Here, ${R_1} = 2\Omega$ , ${R_2} = 2\Omega$ , and ${R_3} = 2\Omega$
Substituting the values in the formula,
$\therefore \dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{2\Omega }} + \dfrac{1}{{2\Omega }} + \dfrac{1}{{2\Omega }}$
$\therefore \dfrac{1}{{{R_{eq1}}}} = \dfrac{3}{{2\Omega }}$
Taking the reciprocal on both sides
$\therefore {R_{eq1}} = \dfrac{{2\Omega }}{3}$
$\therefore {R_{eq1}} = 0.67\Omega$
This is the equivalent resistance of the parallel resistance.
The modified circuit diagram can be shown below

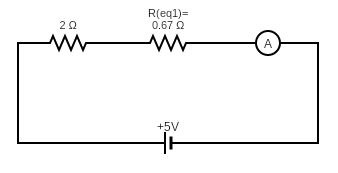
For the series connection of resistors, the equivalent resistance can be found as
${R_{eq2}} = {R_1} + {R_{eq1}}$
Here, ${R_1} = 2\Omega$ , ${R_{eq1}} = 0.67\Omega$
Substituting the values in the formula,
$\therefore {R_{eq2}} = 2\Omega + 0.67\Omega$
$\therefore {R_{eq2}} = 2.67\Omega$
Now, we know that Ohm’s Law states that
$V = IR$
$\therefore I = \dfrac{V}{R}$
Here,
The current $I$ shows the ammeter reading,
The resistance $R$ shows the equivalent resistance = $2.67\Omega$ = $\dfrac{8}{3}\Omega$
The voltage $V$ shows the cell voltage = $5\;V$
Substituting the values in Ohm’s Law
$\therefore I = \dfrac{5}{{\dfrac{8}{3}}}$
We know that denominator’s denominator is shifted to the numerator
$\therefore I = \dfrac{{5 \times 3}}{8}$
$\therefore I = \dfrac{{15}}{8}$
Further simplifying, we get
$\therefore I \approx 2A$
Hence, the correct option is Option $(D)$ .

Note :
While rearranging the circuit diagram, the resistances that are connected between the same ends can be rearranged together as parallel resistances. Also to verify the rearranged circuit, we can check if both ends of any component have the same component as before.