Question

What is the reading of ammeter in adjoining circuit diagram?

Answer 1

An ammeter is an instrument that is commonly used to measure the current in a given circuit. The reading shown by the ammeter is always the same reading that the total amount of current is passing through that segment. Hence, we need to find out the total current in this question.

Complete step-by-step solution:
In this question, we need to find out the reading in ammeter, as we know that ammeter shows the current reading so this means if we find out how much amount of current is flowing through it then we will get the reading in ammeter
To find out the amount of current flowing in this circuit we need to apply Kirchhoff’s Voltage Law (KVL) in this given circuit. As we all know that for KVL we should have to define some current for each of the segment of the given circuit
So, the diagram can be redrawn as

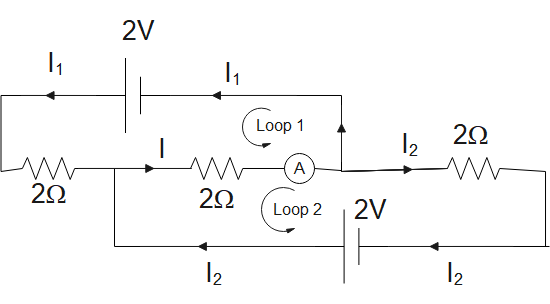
From the above diagram we can say that “I” is the amount of current flowing through the ammeter and
$I\text{ }=~{{I}_{1}}+{{I}_{2}}$ …...……… (a)
Applying K.V.L. in Loop 2 we get,
$2-2I-2{{I}_{2}}=0$
or
$2I+2{{I}_{2}}=2$ ………… (1)
$I=\dfrac{2-2{{I}_{2}}}{2}$ ………………. (2)
Now applying KVL in Loop 1 we get,
$2{{I}_{1}}+2I= 2$ ………….. (3)
Putting the value of “I” from equation (2) we get
$2({{I}_{1}}-{{I}_{2}})=0$
${{I}_{1}}={{I}_{2}}$ ……… (4)
Now putting the value of ${{I}_{1}}$ from equation (4) in equation we get
$I=2{{I}_{2}}$
Putting this value in equation (1) we get
$2(2{{I}_{2}})+2{{I}_{2}}=2$
${{I}_{2}}=\dfrac{1}{3}$
Now since ${{I}_{1}}={{I}_{2}}$
Therefore, ${{I}_{1}}=\dfrac{1}{3}$
Putting both the values in equation (a) we get,
$I\text{ }=~{{I}_{1}}+{{I}_{2}}$
$I=\dfrac{2}{3}A$
Therefore, the current through the ammeter is $\dfrac{2}{3}A$.
So, we can conclude that the ammeter will show a reading of $\dfrac{2}{3}A$

Note: In the above question there were three variables so we need three equations to solve this, but there are only two loops so we can make only two equations using KVL. So, in this case we need to find the third equation by solving both the equations and finding the relation in between two equations