Question

What is the ratio of the reading of the ammeter ${{A}_{1}}$ and ${{A}_{2}}$ in the network shown below?

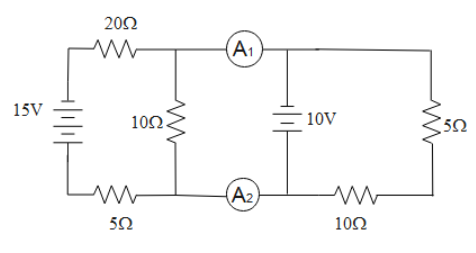
A. $2:1$
B. $4:3$
C.$1:2$
D. $1:1$

Answer 1

The analysis of the circuit is done with the help of the two fundamental laws popularly known as Kirchhoff’s Laws. There are two postulated laws under Kirchhoff’s laws. These laws are named Kirchhoff’s ${{1}^{st}}$law (current law), and Kirchhoff’s ${{2}^{nd}}$ law (voltage law).

Complete answer:
According to Kirchhoff’s ${{1}^{st}}$ law (current law), it is stated that the net algebraic sum of the current at a node is always zero. In other words, the incoming current will be equal to the outgoing current. It is abbreviated as KVL.
The current always flows from the higher potential to the lower potential to balance the two-terminal. So the $15V$ voltage source will be superior.
The current-flow along the branches can be visualized as in the following diagram,

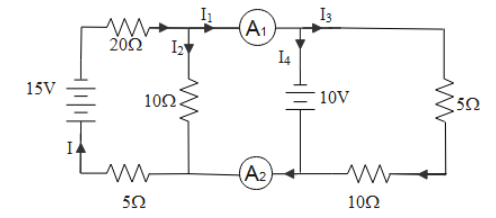
So from the above circuit, the ammeter ${{A}_{1}}$ will show the reading of ${{I}_{1}}$. This current further distributes in branches as ${{I}_{3}}$ and ${{I}_{4}}$. So mathematically we got a relation,
${{I}_{1}}={{I}_{3}}+{{I}_{4}}$
The ammeter ${{A}_{2}}$ will show the reading of current ${{I}_{3}}\And {{I}_{4}}$
${{A}_{{{2}_{reading}}}}={{I}_{3}}+{{I}_{4}}$
From the current distribution in the circuit, it can be said that both the ammeters will show the same reading. So the ratio of this reading will be
${{A}_{1}}:{{A}_{2}}=1:1$

Thus, the correct option to satisfy the question is Option D.

Note:
The sign convention of the current is considered according to the ease of the analyst (the one who is trying to study the nature of the circuit). But the sign configuration should always be in one direction. It's not like that once you consider the current from one side and suddenly you switch the direction of current while applying KCL or KVL.