Question

What is the ratio in which the x-axis divides the line segment joining the points (1, 2) and (2, 3)?
(a). 3:2
(b). 2:3
(c). – 3:2
(d). – 2:3

Answer 1

Hint: The section formula for the point (x, y) which divides the line segment joining the points $({x_1},{y_1})$ and $({x_2},{y_2})$ in the ratio m:n is given as $(x,y) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$. Use this formula to find the ratio in which the x-axis divides the line segment joining the points (1, 2) and (2, 3).

Complete step-by-step answer:
We need to find the ratio in which the x-axis divides the line segment joining the points (1, 2) and (2, 3).
Any point on the x-axis has its y coordinate equal to zero. Hence, let us assume a point (x, 0) that divides the line segment joining the points (1, 2) and (2, 3).
The section formula for the point (x, y) which divides the line segment joining the points $({x_1},{y_1})$ and $({x_2},{y_2})$ in the ratio m:n is given as follows:
$(x,y) = \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right)$

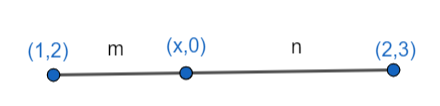
Let the ratio in which the point (x, 0) divides the line segment joining the points (1, 2) and (2, 3) be m:n. then we have:
$(x,0) = \left( {\dfrac{{m(2) + n(1)}}{{m + n}},\dfrac{{m(3) + n(2)}}{{m + n}}} \right)$
Simplifying, we have:
$(x,0) = \left( {\dfrac{{2m + n}}{{m + n}},\dfrac{{3m + 2n}}{{m + n}}} \right)$
The corresponding coordinates are equal. Equating the y-coordinates, we have:
$\dfrac{{3m + 2n}}{{m + n}} = 0$
Simplifying, we have:
$3m + 2n = 0$
$3m = - 2n$
Finding the ratio of m and n, we have:
$\dfrac{m}{n} = \dfrac{{ - 2}}{3}$
Hence, the x-axis divides the line segment joining the points (1, 2) and (2, 3) in the ratio – 2:3.
Hence, the correct answer is option (d).

Note: You can also find the equation of the line segment joining the points (1, 2) and (2, 3) and then find the point of intersection with the x-axis. Then use distance between two points formula $\sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2}}$ to find the ratio.