Question

What is the range of $y=-2\sin \left( x+\pi \right)-3$?

Answer 1

Hint : We first try to plot the graph for $y=\sin x$. We try to find the range of the function and the change for $y=\sin x$ and $y=\sin \left( x+\pi \right)$. Then we multiply with the number $-2$ and subtract 3 to find the range for the function $y=-2\sin \left( x+\pi \right)-3$. We also draw the graph for $y=-2\sin \left( x+\pi \right)-3$.

Complete step-by-step answer :
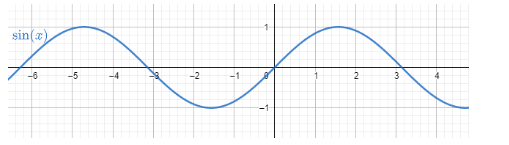
The usual common graph which is easier to plot on the graph is $y=\sin x$.
The graph is an oscillating graph with boundary being $-1$ and 1.
The domain for the graph $y=\sin x$ is $\forall x\in \mathbb{R}$.
The range for the graph $y=\sin x$ is $\left[ -1,1 \right]$.

Now depending on the above-mentioned graph, we are going to first find the graph of
$y=\sin \left( x+\pi \right)$ and then find the graph of $y=-2\sin \left( x+\pi \right)-3$.
The change between $y=\sin x$ and $y=\sin \left( x+\pi \right)$ is that for a particular value of $x$, we are going to find the value of $y$ being equal to the value of $\sin \left( x+\pi \right)$.
This means that we are shifting the same graph on the left side with the value of $\pi$.
The domain for the graph $y=\sin \left( x+\pi \right)$ is $\forall x\in \mathbb{R}$.
The range for the graph $y=\sin \left( x+\pi \right)$ is $\left[ -1,1 \right]$.

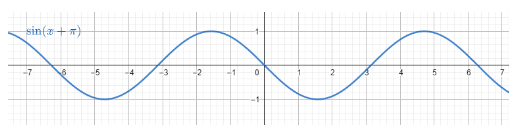
We have the range for $-1\le \sin \left( x+\pi \right)\le 1$.
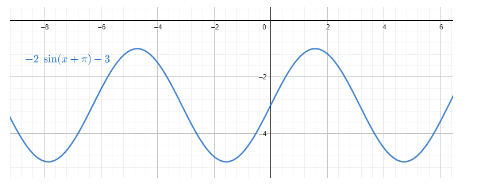
Now we multiply with the number $-2$ and subtract 3 to find the range for the function $y=-2\sin \left( x+\pi \right)-3$.
$\begin{aligned} & -1\le \sin \left( x+\pi \right)\le 1 \\\ & \Rightarrow 2\ge -2\sin \left( x+\pi \right)\ge -2 \\\ & \Rightarrow 2-3\ge -2\sin \left( x+\pi \right)-3\ge -2-3 \\\ & \Rightarrow -1\ge -2\sin \left( x+\pi \right)-3\ge -5 \\\ & \Rightarrow -5\le -2\sin \left( x+\pi \right)-3\le -1 \\\ \end{aligned}$
Therefore, the range of $y=-2\sin \left( x+\pi \right)-3$ is $\left[ -5,-1 \right]$.

Note : We need to be careful about the shift from $y=\sin x$ to $y=\sin \left( x+\pi \right)$. The addition or subtraction of the constant decides the direction of the shift. If the value is positive then the graph shifts left and if the value is negative then it shifts right.