Question

What is the range of the function, $y=\cos \left( x \right)$ ?

Answer 1

The given equation is a ‘cosine’ function. It is one of the most important trigonometric functions and is used in many other areas of math and physics. We will first see the graphical representation of the ‘cosine’ function and then find the range of the cosine function with the help of this graph. We will also see the domain over which a ‘cosine’ function operates.

Complete step by step solution:
The trigonometric function given to us in the problem is: $y=\cos \left( x \right)$. This ‘cosine’ function can be graphically represented as follows:

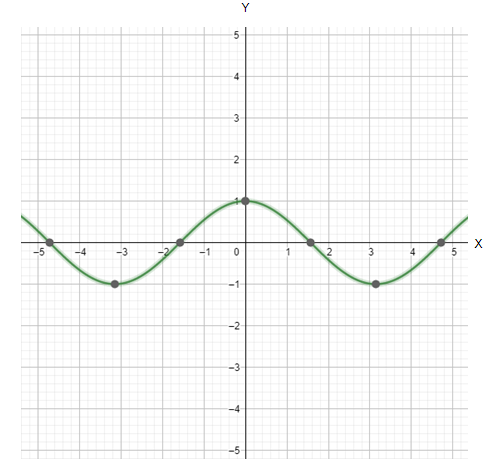
Here, we can first observe that the domain of the ‘cosine’ function starts from negative infinity and goes till positive infinity. Thus, the domain of the cosine function is all the Real numbers.
Additionally, we can observe from the graph that the cosine function gives an output of zero at every odd multiple of $\dfrac{\pi }{2}$.
Now, if we plot the mapping of this ‘cosine’ function, on the Y-axis, that is, collect the projection of all the points of the curve on the Y-axis, we will get its range.
On doing so, we can clearly see that the range of values on the Y-axis varies from -1 to 1, both included.
Thus, the range of our cosine function comes out to be $\left[ -1,1 \right]$.
Hence, the range of the function, $y=\cos \left( x \right)$ comes out to be $\left[ -1,1 \right]$

Note: One should not confuse between the domain and range of any given function. One very simple way to remember the difference between domain and range is, the domain of a function is the set of all the numbers that is acceptable to the function (or, input) and the range of a function is the set of all numbers produced by a function for this domain (or, output).