Question

What is the range of $\cot x$?

Answer 1

Hint : We are given the function $\cot x$ and we need to find its range. The range of a function can be defined as all the outputs obtained after substituting the domain value in the function. We will also try to figure out the range and domain from the graph of $\cot x$. We will define a function $y = \cot x$ and then plot for $x$ and $y$. Range of a function $f$ is represented as $Range\left( f \right)$.

Complete step-by-step answer :
We first see What does domain stand for?
Domain is basically the set of all values that qualify as we input them in a function.
The range of a function is the set of all outputs of a function when domain values are substituted in the function.
Let us consider a function $y = \cot x$
Now, plotting the graph of the function $y = \cot x$.

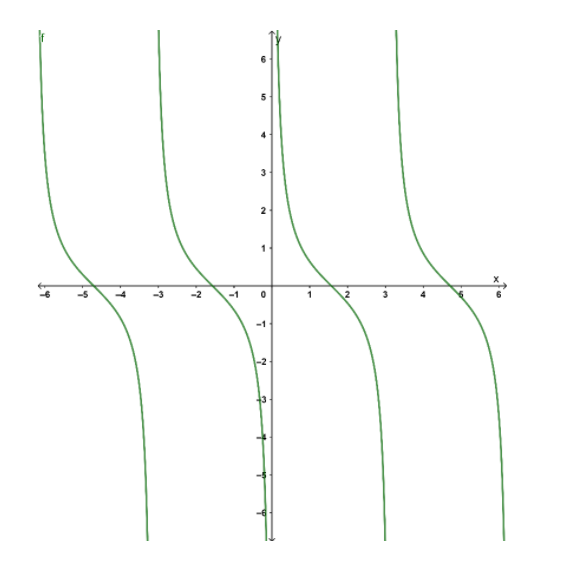
From the graph, we see that the graph is not continuous, which means that the function is not defined on the points where the graph breaks. The points which take the value of $x$ in the graph collectively constitute a domain. And the points which take the value of $y$ together constitute the range of the function.
Since we need to find out the range of the function $\cot x$, we will see what are the values taken by $y$ in the graph. We see that $y$ takes every value on the number line. i.e. for every value of $y$ on the real line, there exists some $x$ such that $y = \cot x$.
Hence, we see that $y$ can take any real value.
So, the range of $y = \cot x$ is the set of real numbers.
Or, we can write it as $Range\left( {\cot x} \right) = \mathbb{R}$, where $\mathbb{R}$ is a set of real numbers.

Note : While finding the range and domain of the function, we need to check where the function is not defined and for that we need to consider each and every point on the real line (Since we are dealing with real numbers only). Basically, for finding the range of a function $y = f\left( x \right)$, we need to check for which value of $y$, there does not exist any $x$ such that $y = f\left( x \right)$. The values of $y$ for which no such $x$ exists will be deleted from the range of the function.