Question

What is the radius of Sodium atom if it crystallizes in BCC unit cell edge length of $400pm$?

Answer 1

The unit cell is the smallest repeating unit of a crystal lattice. There are different types of crystal lattices, out of which one is body-centered cubic BCC which can be seen in the below image:

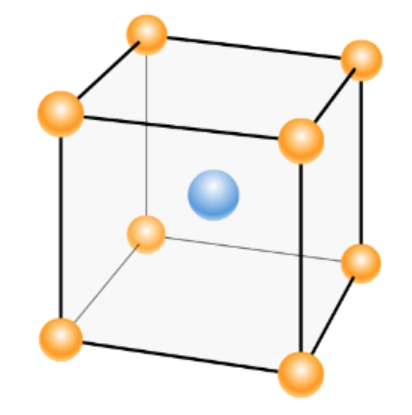
When any atoms are arranged in a body-centered cubic cell, the radius will be determined by substituting the edge length in the below formula.
$r = \dfrac{{\sqrt 3 }}{4} \times a$
$r$ is radius of a body centered cubic unit cell
$a$ is edge length.

Complete answer:
Given that the sodium atom is crystallized in a body-centered cubic cell, with the edge length of $400pm$.
We know the radius formula in BCC as
$r = \dfrac{{\sqrt 3 }}{4} \times a$
Substituting this edge length in the above formula,
$r = \dfrac{{\sqrt 3 }}{4} \times 400$
On simplification, we get the radius as
$r = 173.2pm$
**Thus, the radius of the sodium atom if it crystallizes in BCC unit cell edge length of $400pm$ is $173.2pm$ .

Additional information:
• Crystallography is a branch that deals mainly with crystal structures. According to this concept, the crystal structure is an order of the arrangement of atoms, ions, or molecules.
• The crystal lattice is also known as crystal structure which is nothing but the arrangement of atoms, ions, or molecules in the form of a space lattice.
• They are different types of crystal structures like body-centered cubic (BCC), face-centered cubic (FCC), and hexagonal cubic packing (HCP).

Note:
• While calculating the radius of a crystal lattice, the edge length is usually taken in the units of picometers as these measurements are very minute.
• 1 picometer is equal to $10^{-12}$ meters. Picometers can be simply represented as $pm$.
• If the edge length is given in meters or angstroms, conversion should be made. Where one angstrom is equal to $100$ picometers.