Question

What is the radius of a steel sphere that will float on water with exactly half the sphere submerged? Density of steel is $7.9 \times {10^3}\dfrac{{kg}}{{{m^3}}}$ and surface tension of water is $7 \times {10^{ - 2}}N$.

Answer 1

Forces on the sphere will be ${F_T} + {F_U} = W$
${F_T}$ is the surface tension, ${F_U}$ is the upthrust, $W$ is the weight of the sphere.
putting their respective values in the above equation we will find the radius of the steel sphere.

Formula used:
${F_T} = 2\pi r \times T$ where $T$ is the surface tension multiplied by the total length of the sphere in contact with water i.e. circumference of the circle.
${F_U} = {\rho _w}gV$ where ${\rho _w}$ is fluid density $g$ is the acceleration due to gravity $V$ is the volume of the object immersed.
$W = {V_S}{\rho _S}g$ where ${V_S}$ is the volume of the sphere ${\rho _S}$ is the density of the sphere.

Complete step by step answer:

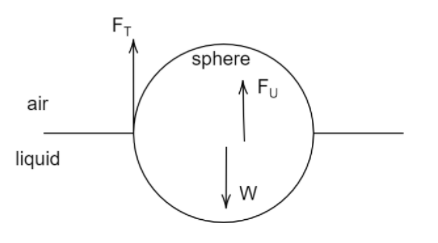
Here a steel sphere is half-submerged in water. ${F_T}$ is the surface tension caused by water on the sphere. ${F_U}$ is the up thrust experienced by the sphere. $W$ is the weight of the steel sphere.
Because it is half-submerged the forces will be balanced
Therefore, ${F_T} + {F_U} = W$
${F_T} = 2\pi r \times T$ where $T$ is the surface tension multiplied by the total length of the sphere in contact with water i.e. circumference of the circle.
${F_U} = {\rho _w}gV$ where ${\rho _w}$ is fluid density $g$ is the acceleration due to gravity $V$ is the volume of the object immersed i.e. of hemisphere $\dfrac{2}{3}\pi {r^3}$.
$W = {V_S}{\rho _S}g$ where ${V_S}$ is the volume of the sphere $\dfrac{4}{3}\pi {r^3}$, ${\rho _S}$ is the density of the sphere
$\Rightarrow 2\pi r \times T + \dfrac{2}{3}\pi {r^3} \times {\rho _w} \times g = \dfrac{4}{3}\pi {r^3} \times {\rho _s} \times g$
$\Rightarrow T = \dfrac{{{r^2}}}{3} \times g\left( {2{\rho _s} - {\rho _w}} \right)$
${\rho _S}$ is given in the question and the density of water is $1$
$\Rightarrow {r^2} = \dfrac{{3T}}{{g(2{\rho _s} - {\rho _w})}}$
$\Rightarrow \dfrac{{7 \times {{10}^{ - 2}} \times 3}}{{10 \times \left( {15.8 - 1} \right) \times {{10}^3}}}$
$\Rightarrow {r^2} = 1.418 \times {10^{ - 2}}$
Hence the radius of the sphere is $r = 1.2 \times {10^{ - 1}}cm$.

Note:
Any item submerged in a fluid or liquid, whether completely or partially, is buoyed up by a force equal to the weight of the fluid displaced by the object. When the surface of a sphere comes into contact with water, surface tension occurs. The upward force exerted by a fluid on an item is known as upthrust. That's why up-thrust works against an object's weight since it has displaced some water since it has half emerged; the sphere is experiencing up thrust.