Question

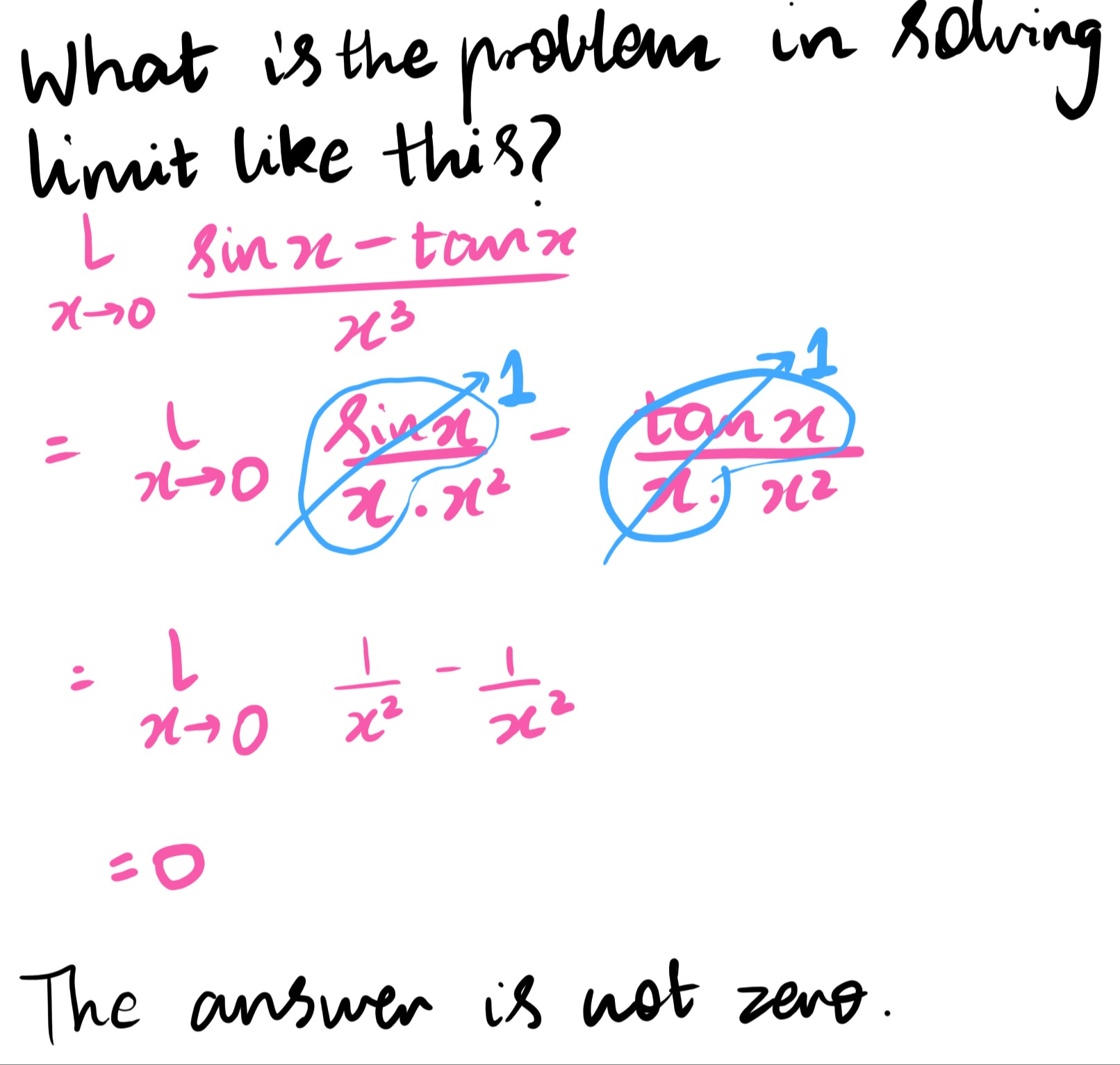
What is the problem in solving limit like this?

$\lim_{x\to0} \frac{sinx-tanx}{x^3}$

= 0

The answer is not zero.

Answer 1

The problem is the incorrect application of limit properties leading to an indeterminate form that is wrongly evaluated. The correct answer is -1/2.

Answer 2

The problem in the provided solution lies in the incorrect application of limit properties. The solution attempts to use the standard limits $\lim_{x\to0} \frac{\sin x}{x} = 1$ and $\lim_{x\to0} \frac{\tan x}{x} = 1$ prematurely.

The expression is $\lim_{x\to0} \frac{\sin x - \tan x}{x^3}$. The provided solution rewrites this as $\lim_{x\to0} \left( \frac{\sin x}{x \cdot x^2} - \frac{\tan x}{x \cdot x^2} \right)$. Then, it replaces $\frac{\sin x}{x}$ with 1 and $\frac{\tan x}{x}$ with 1, leading to $\lim_{x\to0} \left( \frac{1}{x^2} - \frac{1}{x^2} \right)$. The error occurs in this replacement step. While $\lim_{x\to0} \frac{\sin x}{x} = 1$ and $\lim_{x\to0} \frac{\tan x}{x} = 1$, these equalities hold only in the limit sense. Replacing $\frac{\sin x}{x}$ and $\frac{\tan x}{x}$ with the constant value 1 within the expression before the limit is fully evaluated is incorrect, especially when they are multiplied by a term like $\frac{1}{x^2}$ which tends to infinity as $x \to 0$.

Specifically, the property $\lim_{x\to a} (f(x) - g(x)) = \lim_{x\to a} f(x) - \lim_{x\to a} g(x)$ is only valid if the individual limits $\lim_{x\to a} f(x)$ and $\lim_{x\to a} g(x)$ exist and are finite. In this case, if we consider $f(x) = \frac{\sin x}{x^3} = \frac{\sin x}{x} \cdot \frac{1}{x^2}$ and $g(x) = \frac{\tan x}{x^3} = \frac{\tan x}{x} \cdot \frac{1}{x^2}$, then $\lim_{x\to0} f(x) = \lim_{x\to0} \frac{\sin x}{x} \cdot \lim_{x\to0} \frac{1}{x^2} = 1 \cdot \infty = \infty$ and $\lim_{x\to0} g(x) = \lim_{x\to0} \frac{\tan x}{x} \cdot \lim_{x\to0} \frac{1}{x^2} = 1 \cdot \infty = \infty$. The original limit is of the indeterminate form $\infty - \infty$. The student incorrectly assumes that $\infty - \infty = 0$.

The correct approach requires evaluating the limit of the entire expression together, for example, by using Taylor series expansions or L'Hopital's rule.

Using Taylor series expansions around $x=0$: $\sin x = x - \frac{x^3}{6} + O(x^5)$ $\tan x = x + \frac{x^3}{3} + O(x^5)$ $\sin x - \tan x = (x - \frac{x^3}{6}) - (x + \frac{x^3}{3}) + O(x^5) = -\frac{x^3}{6} - \frac{x^3}{3} + O(x^5) = -\frac{3x^3}{6} + O(x^5) = -\frac{x^3}{2} + O(x^5)$

So, $\lim_{x\to0} \frac{\sin x - \tan x}{x^3} = \lim_{x\to0} \frac{-\frac{x^3}{2} + O(x^5)}{x^3} = \lim_{x\to0} \left(-\frac{1}{2} + O(x^2)\right) = -\frac{1}{2}$.

The problem in the solution is the incorrect application of limit properties when dealing with indeterminate forms involving infinity. The standard limits $\lim_{x\to0} \frac{\sin x}{x}=1$ and $\lim_{x\to0} \frac{\tan x}{x}=1$ are based on the leading term of the Taylor series expansion. For this limit, where the denominator is $x^3$, we need to consider higher-order terms in the expansion of the numerator. Replacing $\frac{\sin x}{x}$ and $\frac{\tan x}{x}$ with 1 is equivalent to using the approximation $\sin x \approx x$ and $\tan x \approx x$, which is too crude for this limit problem.

The final answer is $\boxed{-1/2}$.

Explanation of the solution: The provided solution incorrectly applies limit properties. It replaces terms $\frac{\sin x}{x}$ and $\frac{\tan x}{x}$ with their limit (1) while they are multiplied by $\frac{1}{x^2}$, which tends to infinity. This leads to an indeterminate form $\infty - \infty$, which is then incorrectly evaluated as 0. The property $\lim(f(x) - g(x)) = \lim f(x) - \lim g(x)$ is valid only if the individual limits exist and are finite. Correct evaluation requires methods like Taylor series expansion or L'Hopital's rule, which yield the limit $-\frac{1}{2}$.