Question

What is the probability that exactly one of them is female and exactly one is a child?
This is the table for the number of people:

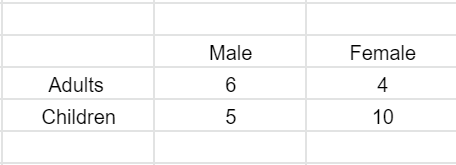
How do I find the probability that exactly one is female and one is a child? Are these independent probabilities or not?

Answer 1

We are first going to explain the concept of probability. Then we need to determine the probability that exactly one person picked from the group of people is a female. Then we calculate the probability of exactly one being a child. Then depending on the relation between the two probabilities obtained, we determine if the probabilities are independent or not.

Complete step-by-step solution:
In order to solve this question, let us first explain the concept of probability. Probability is the possibility of the occurrence of an event. It can be defined as the number of favourable outcomes divided by the total number of outcomes.
$\Rightarrow P\left( E \right)=\dfrac{\text{No}\text{. of favourable outcomes}}{\text{Total number of outcomes}}$
Now for the given question, we are required to calculate the probability that exactly one of them is a female. For this let us consider the event as selecting a person from the group of people and the favourable outcome be that the selected person be a female.
The total number of people in the group can be calculated by adding the columns from the table,
$\Rightarrow \text{Total no}\text{. of people=No}\text{. of males + No}\text{. of females}$
The number of males is given in the first column and the number of females is given in the second column.
$\Rightarrow \text{Total no}\text{. of people=}\left( 6+5 \right)+\left( 4+10 \right)$
$\Rightarrow \text{Total no}\text{. of people=}25$
The number of females in the group can be calculated by adding the terms in the second female column.
$\Rightarrow \text{No}\text{. of females=4+10=14}$
Probability that exactly one of them is a female can be obtained by dividing the no. of females by the total number of people.
$\Rightarrow {{P}_{one-female}}=\dfrac{14}{25}=0.56$
Hence, the probability that exactly one of them is a female is 0.56.
We calculate for the probability of exactly one child in a similar manner.
The total number of people in the group can be calculated by adding the rows from the table,
$\Rightarrow \text{Total no}\text{. of people=No}\text{. of adults + No}\text{. of children}$
The number of adults is given in the first row and the number of children is given in the second row.
$\Rightarrow \text{Total no}\text{. of people=}\left( 6+4 \right)+\left( 5+10 \right)$
$\Rightarrow \text{Total no}\text{. of people=}25$
The number of children in the group can be calculated by adding the terms in the second row.
$\Rightarrow \text{No}\text{. of children=5+10=15}$
Probability that exactly one of them is a child can be obtained by dividing the no. of children by the total number of people.
$\Rightarrow {{P}_{one-child}}=\dfrac{15}{25}=0.6$
Hence, the probability that exactly one of them is a child is 0.60.
Since the two events don’t depend on each other, they are called independent probabilities.

Note: Probability is a very important concept required to solve such sums. It plays a very important role in prediction and in everyday scenarios. The number of favourable outcomes depends on the event for which we are calculating the probability.