Solveeit Logo
Login

Question

Question: What is the principal value of \({{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\l...

What is the principal value of cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) ?

Explanation

Solution

Hint: For solving this question first, we will go through some important aspects like domain and range of the inverse trigonometric functions y=cos⁡−1xy={{\cos }^{-1}}x and y=sin⁡−1xy={{\sin }^{-1}}x . First, we will use one of the basic formulas of the trigonometric ratio to write cos⁡2π3=−12\cos \dfrac{2\pi }{3}=-\dfrac{1}{2} in the given term. After that, we will use one of the basic formula of inverse trigonometric functions, i.e. cos⁡−1(−12)=2π3{{\cos }^{-1}}\left( -\dfrac{1}{2} \right)=\dfrac{2\pi }{3} to find the value of cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) . After that, we will use formula sin⁡2π3=32\sin \dfrac{2\pi }{3}=\dfrac{\sqrt{3}}{2} and sin⁡−1(32)=π3{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{3} to find the value of sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) . Then, we will easily find the value of cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) .

Complete step-by-step solution -
Given:
We have to find the principal value of the following:
cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right)
Now, we will find the principal values of cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) and sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) separately and then, we will add them to find the principal value of cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) .
Calculation for the principal value of cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) :
Now, before we proceed we should know about the inverse trigonometric function y=cos⁡−1xy={{\cos }^{-1}}x . For more clarity look at the figure given below:

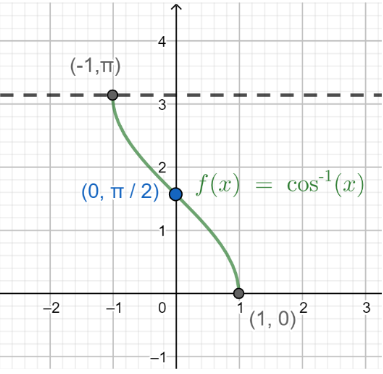
In the above figure, the plot y=f(x)=cos⁡−1xy=f\left( x \right)={{\cos }^{-1}}x is shown. And we should know that the function y=cos⁡−1xy={{\cos }^{-1}}x is defined for x∈[−1,1]x\in \left[ -1,1 \right] and its range is y∈[0,π]y\in \left[ 0,\pi \right] then, yy is the principal value of cos⁡−1x{{\cos }^{-1}}x .
Now, we will use the above concept for giving the correct principal value of cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) .
Now, before we proceed further we should know the following formulas:
cos⁡2π3=cos⁡(π−π3)=−cos⁡π3=−12..................(1) cos⁡−1(−12)=2π3...........(2) \begin{aligned} & \cos \dfrac{2\pi }{3}=\cos \left( \pi -\dfrac{\pi }{3} \right)=-\cos \dfrac{\pi }{3}=-\dfrac{1}{2}..................\left( 1 \right) \\\ & {{\cos }^{-1}}\left( -\dfrac{1}{2} \right)=\dfrac{2\pi }{3}...........\left( 2 \right) \\\ \end{aligned}
Now, we will use the above two formulas to solve this question.
We have, cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) .
Now, we will use the formula from the equation (1) to write cos⁡2π3=−12\cos \dfrac{2\pi }{3}=-\dfrac{1}{2} in the term cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) . Then,
cos⁡−1(cos⁡2π3) ⇒cos⁡−1(−12) \begin{aligned} & {{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) \\\ & \Rightarrow {{\cos }^{-1}}\left( -\dfrac{1}{2} \right) \\\ \end{aligned}
Now, we will use the formula from the equation (2) to write cos⁡−1(−12)=2π3{{\cos }^{-1}}\left( -\dfrac{1}{2} \right)=\dfrac{2\pi }{3} in the above line. Then,
cos⁡−1(−12) ⇒2π3 \begin{aligned} & {{\cos }^{-1}}\left( -\dfrac{1}{2} \right) \\\ & \Rightarrow \dfrac{2\pi }{3} \\\ \end{aligned}
Now, from the above result, we conclude that the principal value of the expression cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) will be equal to 2π3\dfrac{2\pi }{3} . Then,
cos⁡−1(cos⁡2π3)=2π3.....................(3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)=\dfrac{2\pi }{3}.....................\left( 3 \right)
Calculation for the principal value of sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) :
Now, before we proceed we should know about the inverse trigonometric function y=sin⁡−1xy={{\sin }^{-1}}x . For more clarity look at the figure given below:

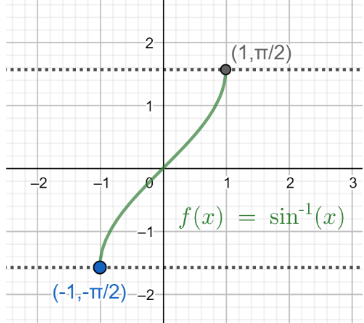
In the above figure, the plot y=f(x)=sin⁡−1xy=f\left( x \right)={{\sin }^{-1}}x is shown. And we should know that the function y=sin⁡−1xy={{\sin }^{-1}}x is defined for x∈[−1,1]x\in \left[ -1,1 \right] and its range is y∈[−π2,π2]y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right] then, yy is the principal value of sin⁡−1x{{\sin }^{-1}}x .
Now, we will use the above concept for giving the correct principal value of sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) .
Now, before we proceed further we should know the following formulas:
sin⁡2π3=sin⁡(π−π3)=sin⁡π3=32.................(4) sin⁡−1(32)=π3...........(5) \begin{aligned} & \sin \dfrac{2\pi }{3}=\sin \left( \pi -\dfrac{\pi }{3} \right)=\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}.................\left( 4 \right) \\\ & {{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{3}...........\left( 5 \right) \\\ \end{aligned}
Now, we will use the above two formulas to solve this question.
We have, sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) .
Now, we will use the formula from the equation (4) to write sin⁡2π3=32\sin \dfrac{2\pi }{3}=\dfrac{\sqrt{3}}{2} in the term sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) . Then,
sin⁡−1(sin⁡2π3) ⇒sin⁡−1(32) \begin{aligned} & {{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) \\\ & \Rightarrow {{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) \\\ \end{aligned}
Now, we will use the formula from the equation (5) to write sin⁡−1(32)=π3{{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right)=\dfrac{\pi }{3} in the above line. Then,
sin⁡−1(32) ⇒π3 \begin{aligned} & {{\sin }^{-1}}\left( \dfrac{\sqrt{3}}{2} \right) \\\ & \Rightarrow \dfrac{\pi }{3} \\\ \end{aligned}
Now, from the above result, we conclude that the principal value of the expression sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) will be equal to π3\dfrac{\pi }{3} . Then,
sin⁡−1(sin⁡2π3)=π3.....................(6){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right)=\dfrac{\pi }{3}.....................\left( 6 \right)
Now, we will use the result of the equation (3) and (6) to find the principal value of cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) . Then,
cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3) ⇒2π3+π3 ⇒π \begin{aligned} & {{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) \\\ & \Rightarrow \dfrac{2\pi }{3}+\dfrac{\pi }{3} \\\ & \Rightarrow \pi \\\ \end{aligned}
Now, from the above result, we conclude that principal value of the cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) is equal to π\pi .
Thus, cos⁡−1(cos⁡2π3)+sin⁡−1(sin⁡2π3)=π{{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right)+{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right)=\pi .

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, we should avoid writing sin⁡−1(sin⁡2π3)=2π3{{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right)=\dfrac{2\pi }{3} directly and use the basic concepts of domain and range of the inverse trigonometric functions y=cos⁡−1xy={{\cos }^{-1}}x and y=sin⁡−1xy={{\sin }^{-1}}x correctly. And after giving calculating the values of cos⁡−1(cos⁡2π3){{\cos }^{-1}}\left( \cos \dfrac{2\pi }{3} \right) and sin⁡−1(sin⁡2π3){{\sin }^{-1}}\left( \sin \dfrac{2\pi }{3} \right) , we should check for the validity of our answer by checking whether it lies in the range of its inverse trigonometric function or not.