Question
Question: What is the potential difference between B and D A. \(\dfrac{1}{{13}}\;V\) B. \(\dfrac{2}{{13}}...
What is the potential difference between B and D
A. 131V
B. 132V
C. 137V
D. 136V
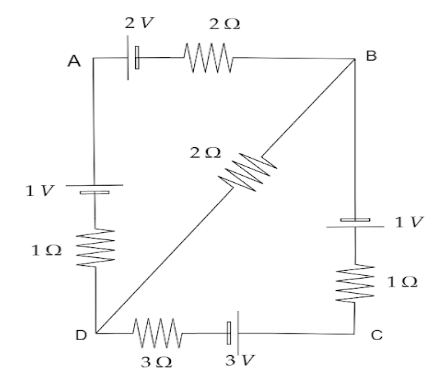
Solution
In this question we have to find the potential difference between two pints. We have to consider two currents i and i′ flowing into the circuit. Then by using Kirchhoff’s Voltage Law we will eventually form equations. By solving the equations, we will find the desired results.
Complete step by step answer:
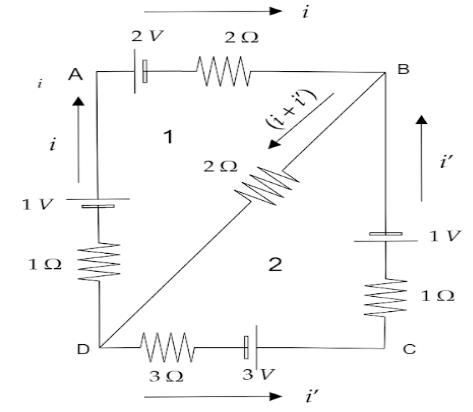
Let us consider two loops 1 and 2. The current flowing through loop 1 is i and the current flowing in loop 2 be i′. The potential at B be Vb and at D be Vd.
Now using Kirchhoff’s Voltage Law we will find out,
Considering loop 1 we formulate the equation,
−(i×1)+1−2−(2i)−2(i+i′)=0
Now, solving the equation we get,
5i+1+2i′=0−−−−−−(1)
Considering loop 2 we formulate the equation as,
−(i′×1)−1+3−(3i′)−2(i+i′)=0
Solving the equation we get,
−2i−6i′+2=0−−−−−−(2)
Multiplying equation (1) by 3 we get,
15i+3+6i′=0−−−−−(3)
Adding equation (2) and equation (3) we get,
13i+5=0
So, we get the value of i=−135.
Putting the value of i in equation (1) we get,
5(−135)+1+2i′=0
Therefore, the value of i′=136.
The current flowing along B and D is =(i+i′)=136−135=131 A.
Now, with the help of Ohm’s Law we will find out the potential difference between B and D.
Vb−Vd=(i+i′)×2 ∴Vb−Vd=132 V
Therefore, the potential difference between the two points is 132 V.
Hence, the correct answer is option B.
Note: It must be noted that in this question we have used Kirchhoff's Voltage Law. The direction of current or the signs we use while formulating the equation follows the rule that if the current exists anything with a positive sign it is considered to be positive and vice-versa. The positive and negative potential of a battery is not decided by the current but by the battery itself.
