Question

What is the potential difference between A and B?

A. 8.4V
B. 2.4V
C. 4.2V
D. 7.2V

Answer 1

As a first step, we could find the effective resistance of all the resistors in the circuit. Then you could find the net current in the circuit using the Ohm’s law. After that you could apply Kirchoff’s voltage law in the loop including AB and the voltage source and thus find the potential difference across AB.

Complete Step by step solution:
In the question, we are given a circuit consisting of few resistors and a cell of voltage 10V and are asked to find the potential difference between A and B.

In order to answer this question, the very first step that we have to follow is to find the net current flowing through the circuit. For finding that, we have to find the equivalent resistance of the circuit.

From the figure we see that the $5\Omega$ resistor and the$2.5\Omega$ are in series, we could redraw the circuit as,

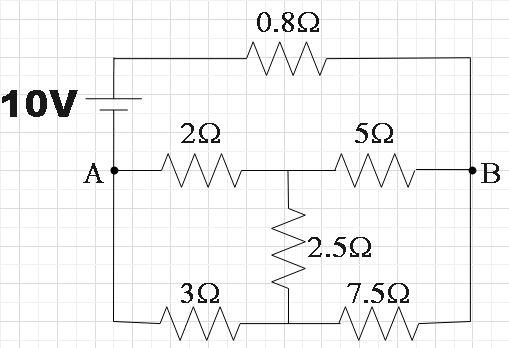
Now we see that,
$\dfrac{2}{5}=\dfrac{3}{7.5}$
Which we know is the Wheatstone bridge condition, so, we find that no current will pass through the$2.5\Omega$. Now, we see that $2\Omega$ resistor and $5\Omega$ resistors are in series with each other, so are the $3\Omega$ and $7.5\Omega$ resistors. So, the circuit can now be reduced as,

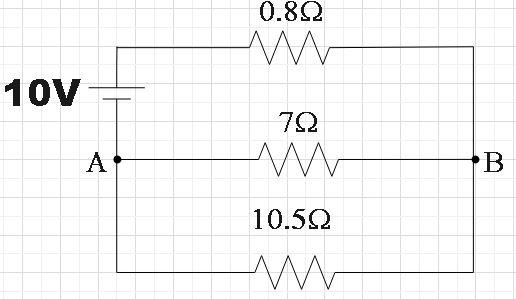
Now we see that $10.5\Omega$ and $7\Omega$ are parallel to each other and $0.8\Omega$ is connected in series with them. So, their equivalent resistance will be,
$R=\dfrac{10.5\times 7}{10.5+7}+0.8$
$\Rightarrow R=\left( 4.2+0.8 \right)\Omega$
$\therefore R=5\Omega$

So we found the net resistance of the given circuit to be$5\Omega$. Net current would then be,
$I=\dfrac{V}{R}$
$\Rightarrow I=\dfrac{10}{5}$
$\therefore I=2A$

Now, from Kirchoff’s voltage rule, we have,
$10-I\left( 0.8\Omega \right)-{{V}_{AB}}=0$
$\Rightarrow 10-2\left( 0.8\Omega \right)={{V}_{AB}}$
$\Rightarrow {{V}_{AB}}=10-1.6$
$\therefore {{V}_{AB}}=8.4V$

Therefore, we found the voltage across the terminals A and B to be $8.4V$.

Hence, option A is found to be the correct answer.

Note:
You may have noted that we have used the Wheatstone bridge principle while finding the effective resistance. On keeping a galvanometer in place of the $2.5\Omega$ resistor, you may observe null deflection. Then we have used the Kirchoff’s voltage rule which states that the net voltage in a loop is zero.