Question
Question: What is the potential difference between \(A\) and \(B\) ? A. \(8.4{\text{ V}}\) B. \(2.4{\text...
What is the potential difference between A and B ?
A. 8.4 V
B. 2.4 V
C. 4.2 V
D. 7.2 V
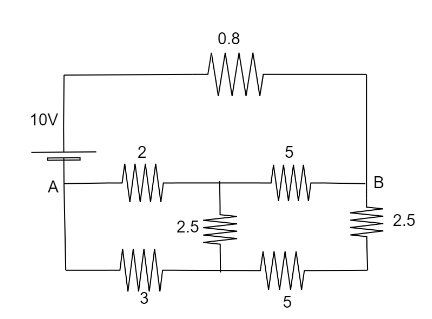
Solution
In the question, try to identify the Wheatstone Bridge. Calculate the equivalent resistance by identifying whether the different resistors are in series or parallel connection. Find the current flowing in the circuit from the basic relations between voltage, resistance and current using Ohm’s Law. Finally using the value of current find the potential difference between A and B.
Complete step by step answer:
Let us identify the Wheatstone bridge. Wheatstone Bridge is a resistance bridge circuit that consists of four arms of resistances. The ratio of resistance of two arms with the other two arms are equal. It works on the principle of null deflection and no current flows through this circuit since the ratio of resistances are equal.In the given circuit, the lower part of the circuit forms a Wheatstone bridge since the ratio of the resistances is equal.
r2r1=r4r3
⇒57.5=23=1.5
Also, the current flowing through resistance of r5=2.5 Ω will be zero.Therefore, we will neglect the resistance of r5.Calculating equivalent resistance,
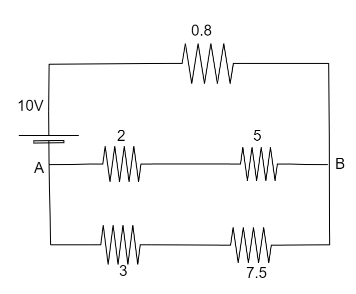
Let,
{r_1} = 7.5{\text{ }}\Omega \\\
\Rightarrow {{\text{r}}_2} = 5{\text{ }}\Omega \\\
\Rightarrow {{\text{r}}_3} = 3{\text{ }}\Omega \\\
\Rightarrow {{\text{r}}_4} = 2{\text{ }}\Omega \\\
\Rightarrow {{\text{r}}_5} = 0.8{\text{ }}\Omega \\\
⇒Req=r5+(r1+r3)+(r2+r4)(r1+r3)×(r2+r4)
The resistance r1 , r3 are in series combination and r2 , r4 are in series and combination, (r1+r3) and (r2+r4) are in parallel.
Req=0.8+(7.5+3)+(3+2)(7.5+3)×(3+2) ⇒Req=5 Ω
According to Ohm’s Law, the current flowing in a circuit is directly proportional to the potential difference and inversely proportional to the resistance in the circuit.
I=ReqV
⇒I=510=2 A
The potential difference between A and B is
P=V−I×r6
⇒P=10−2×0.8
∴P=8.4 V
The potential difference between A and B is 8.4 V.
Therefore, the correct answer is option A.
Note: The question becomes easier only if you correctly identify the Wheatstone Bridge. While calculating the potential difference between A and B only consider the resistance that lies between them. The Wheatstone bridge is very useful. It makes it much easier and precise to detect a null (zero current) than measure the actual value of current. The ratio metric nature of the bridge means that certain internal errors will cancel out. The bridge circuit can be used in one of two ways. The first is to adjust component values until the bridge is balanced. This is typically used to determine the value of an unknown resistor in the bridge when the other three resistances are known. The second method is to measure changes in the output voltage across the bridge when one of the resistances is subject to externally-applied changes of some kind.
