Question

What is the phase difference between AC e.m.f and current in the following?
Pure resistor and pure inductor.

Answer 1

Hint To find the given values we have to treat all the voltmeters and ammeters as a set of resistances.
Then we have to obtain voltage differences and current across each section.

Complete step-by-step solution :
1. In the case of a pure resistor the e.m.f and current are both in the same phase. It is shown in the given diagram

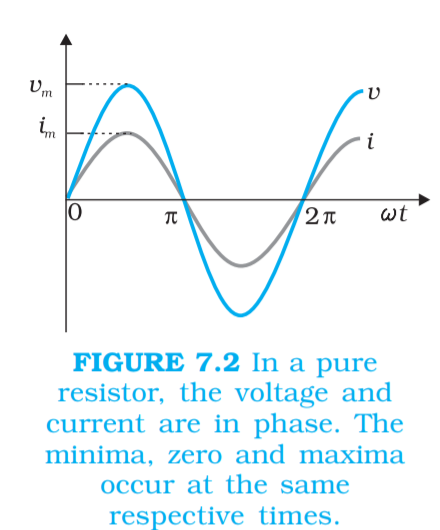
Here by kirchoff’s loop law,
${V_m}\sin \omega t = iR$
$i = ({V_m}/R)\sin \omega t \\\ i = {i_m}\sin \omega t \\\$
2. So the phase difference $\phi$ between both the e.m.f and current is ${0^o}$
In the case of pure inductor the e.m.f leads the current by ${90^o}$. It is shown in the given diagram

Here by the kirchoff’s law,

$$\int {di/dt} dt = {V_m}/L\int {\sin (\omega t)dt} \\\ i = {V_m}\cos (\omega L)/\omega L + cons\tan t \\\$$

After the integration
$i = {i_m}\sin (\omega t - \pi /2)$

Hence the phase difference is ${90^o}$.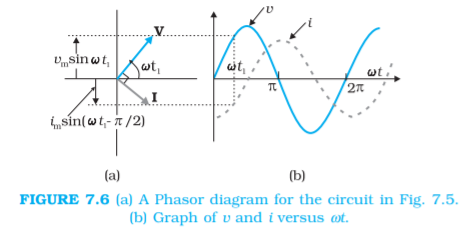

Note:- Here all the equations should be obtained step by step. The integration should be done independently and subsequently.