Solveeit Logo
Login

Question

Question: What is the perpendicular slope of 3?...

What is the perpendicular slope of 3?

Explanation

Solution

The given slope of the line is 3. We can find the perpendicular slope of this line by finding the slope of the line which is perpendicular to the original line. Let m1{{m}_{1}} be the slope of the first line and let m2{{m}_{2}} be the slope of the second line or the line perpendicular to the first line. We can find the slope of the line perpendicular to the original line by using the formula,
 m1m2=−1 ⇒m2=−1m1 \begin{aligned} & \,{{m}_{1}}{{m}_{2}}=-1 \\\ & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\\ \end{aligned}

Complete step-by-step solution:

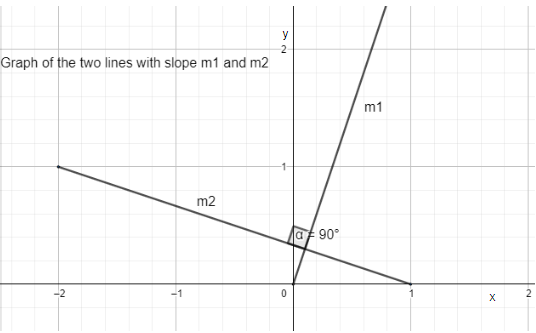
The slope of a straight line is defined as the ratio of the change in y-coordinate of the line to the change in x-coordinate of the line. Slope can also be defined as the tangent of the angle made by the line with the x-axis. If two lines are perpendicular, it implies they intersect at 90∘{{90}^{\circ }} at the point of intersection.
Let us assume m1{{m}_{1}} to be the slope of the first line or the line given to us in the question. Hence we can see that m1=3{{m}_{1}}=3 , is given to us in the question. Let us assume m2{{m}_{2}} to be the slope of the second line or the line which is perpendicular to the given line. We can find the slope of the second line by using the formula for two perpendicular lines in Cartesian plane, which is,
 m1m2=−1 ⇒m2=−1m1 \begin{aligned} & \,{{m}_{1}}{{m}_{2}}=-1 \\\ & \Rightarrow {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\\ \end{aligned}
Therefore, we get,
m2=−13{{m}_{2}}=-\dfrac{1}{3}
The slope of the line perpendicular to 3 is −13-\dfrac{1}{3} .

Note: While the formula for slope of two perpendicular lines works well for almost all cases, one should be careful when the slope of a line is given as 0. In this case we get,
m2=−1m1 m2=−10 \begin{aligned} & {{m}_{2}}=-\dfrac{1}{{{m}_{1}}} \\\ & {{m}_{2}}=-\dfrac{1}{0} \\\ \end{aligned}
Which means that m2{{m}_{2}} is infinity. In reality, this means that the line is vertical since the inverse tangent of infinity is 90∘{{90}^{\circ }} which means it is perpendicular to x-axis and parallel with the y-axis. Any line parallel to the y-axis and perpendicular to x-axis will have a slope of infinity.