Question

What is the perpendicular distance of the point (x, y) from x-axis?
(a) x
(b) y
(c) |x|
(d |y|

Answer 1

Hint:To solve this question, we will form different cases on the basis of which quadrant the point is present. Then, in all these cases, we will find out the perpendicular distance of a point from the x-axis, and then we will obtain a general relation between the distance of the point from the x-axis and the values of the x – coordinate and y – coordinate.

Complete step-by-step answer:
Before solving the question, we must know what the x-axis is. the x-axis is the horizontal axis of a system of coordinates. the x-axis contains the value of all the real numbers. Now, we have to find the perpendicular distance of the point (x, y) from the x-axis. The distance of the point from the x-axis will depend on, in which quadrant the point is present. Thus, we will form the following cases according to the point (x, y).
Case 1: (x, y) is present in the first quadrant. This is shown in the figure below.

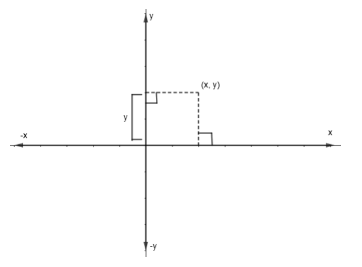
Here, we can see that the perpendicular distance of the point (x, y) from the x-axis is y.
Case 2: (x, y) is present in the second quadrant. This is shown in the figure below.

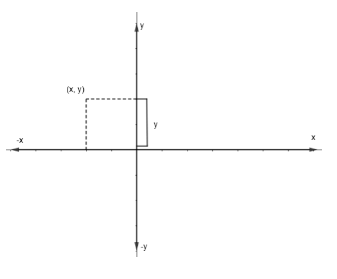
In this case, the perpendicular distance of the point (x, y) from the x-axis is y.
Case 3: (x, y) is present in the third quadrant. This is shown in the figure below.

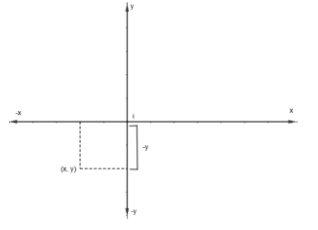
In this case, we have taken distance as – y because y is already negative in the third quadrant and the distance should always be positive.
Case 4: (x, y) is present in the fourth quadrant. This is shown in the figure below.

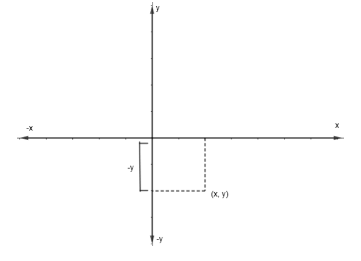
Similar to case 3, the distance will be – y and the distance should be always positive.
From all the above cases, we can see that the distance of (x, y) from the x-axis is equal to the absolute value of y. Thus the perpendicular distance = |y|.
Hence, option (d) is the right answer.

Note: If the point in the question had been in 3 dimensions, then the distance of the point from the x-axis would have been equal to $\sqrt{{{y}^{2}}+{{z}^{2}}}$ where y and z are the other two axes. In this situation, irrespective of the quadrant in which the point is present, the distance would be equal to $\sqrt{{{y}^{2}}+{{z}^{2}}}.$