Question
Question: What is the perpendicular distance of point \[\left( {4,3} \right)\] from x- axes....
What is the perpendicular distance of point (4,3) from x- axes.
Solution
First we need to recognize or identify the x and y coordinates from a given point. The x-coordinate of the given point is the perpendicular distance of the given point from the y-axis. The y-coordinate of the given point is the perpendicular distance of the given point from the x-axis.
Complete step by step answer:
Let p(x,y) be any point, since the perpendicular distance from y-axis to a point p(x,y) is x-coordinate value and also distance is always positive quantity, Hence, ∣x∣ is the distance.
Similarly, the perpendicular distance from x-axis to a pointp(x,y) is y-coordinate
Value. Hence, ∣y∣ is the distance.
In a given point (4,3), x-coordinate is 4 and y-coordinate is 3.
Also, the absolute values of x and y coordinates are 4and 3 respectively.
The point (4,3) is located in the coordinate plane as shown in the graph below.
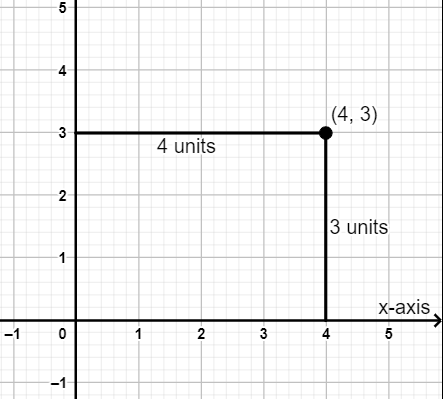
clearly, the perpendicular distance from y-axis to a point(4,3) is 4 and the perpendicular distance from x-axis to a point(4,3) is 3.
Hence the perpendicular distance of point (4,3) from x-axes is 3units.
Note:
Note that the lines which are perpendicular to the x-axis are all parallel to the y-axis and they are also known as vertical lines. The lines which are perpendicular to the y-axis are all parallel to the x-axis and they are also known as horizontal lines.
The abscissa of any point (x,y) is x-coordinate and the ordinate of any point (x,y) is y-coordinate. We use “abscissa” and “ordinate” terms in the solution.
