Question

What is the period of the function $f\left( x \right)=\sin x?$

Answer 1

To know the period of the function $\sin x$. First of all, we need to know what is the period in the trigonometric function?
The period of the trigonometric function is the length of a cycle is called the period. In other words, we can say that period is the distance between the repetition of any function. It’s also known as the length from one point to the next point.
Generally, we have three basic functions of trigonometry that are $\sin x$, $\cos x$, and $\tan x$. Each function of them has a different period.
The period is represented by the capital letter of the English alphabet ‘T’.
To get the period of any function (in some cases) just plots a graph of that function we will get the period of that function.

Complete step by step solution:
The given function is $f\left( x \right)=\sin x$
We know that the period of the function $f\left( x \right)=\sin nx$ is $\dfrac{2\pi }{n}$.
And in the given function $f\left( x \right)=\sin x$ we can say that $n=1$
Therefore, the period will be $\dfrac{2\pi }{1}=2\pi$

In another word, we can see in the graph of the sine function we will notice that the curve is repeated after $2\pi$angle, so we can say that the period $f\left( x \right)=\sin x$is $2\pi$.

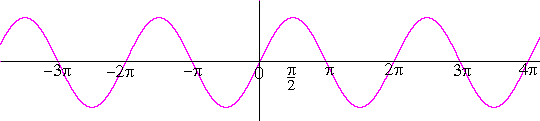
Note:
The sine function is the periodic function and the domain of this function is $\left( -\infty,\infty \right)$and the range of this function is $\left[ -1,1 \right]$.
The sine function is symmetry about origin because it’s an odd function.