Question
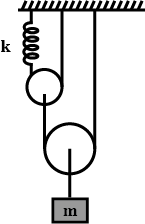
Question: What is the period of small oscillations of the block of mass m, if the springs are ideal and pulley...
What is the period of small oscillations of the block of mass m, if the springs are ideal and pulleys are massless?
A) 2πkm
B) 2π2km
C) 2πk2m
D) πkm
Solution
First find the spring constant and then by using the equation that gives the time period of oscillation of a spring in relation to mass of the body and the spring constant find the weight of the body. Here first we will draw the free body diagram of the given system as shown below. And then after balancing the force as discussed below.
Complete step by step solution:

Free body diagram of given pulley-block system as shown in below figure.
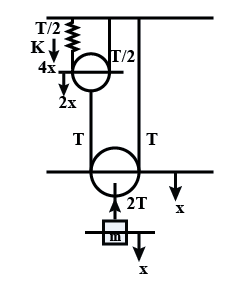
⇒ 2T = mg
By using Hooke's law for a spring balance.
⇒ mg =4kx0 ………….. (1)
⇒ 2T=kx0
⇒ T=2kx0
If displaced
⇒ mg−2T = ma
⇒ mg−4k(x0+x) = ma
⇒ 2T= k(x0+x)
⇒ T = 2k(x0+x)
Now,
From equation (1), we will get
⇒ mg =4kx0
⇒ x0=4kmg
As we know,
⇒ ω=x0g
Put x0=4kmgand get
⇒ ω=4kmgg
⇒ ω=m4k
Now, by using the formula of time period as T=ω2π
Put the value of ω=m4kand we will get
⇒ T=2π4km
∴ T=πkm
Thus, T=πkm is the period of small oscillations of the block of mass m.
Therefore, option (D) is the correct option.
Note: Mathematically, Hooke's law for a spring balance can be written down as:
F= -kx
Where F is the restoring force,
k is the spring constant of the spring balance and
x is the displacement from the initial position of the spring balance system.
This formula is extremely useful in other chapters also like Simple Harmonic Chapter, Newton's Laws of Motion, etc.
