Question

What is the period of $f\left( t \right)=\cos \left( 10t \right)$ ?

Answer 1

To solve this question we need to have the concept of trigonometric function and its period. In this question we are given the trigonometric function $\cos$. The period of the function $\cos x$ is $2\pi$, which means the value of the trigonometric function $\cos x$ repeats itself after $2\pi$.

Complete step by step solution:
The question asks us to find the period for the trigonometric function $\cos$ in the question given to the angle in the $\cos$ function is $10t$. To start with the question, first let us understand the meaning of period. The distance between the repetition of any function is called the period of the function. For a trigonometric function, the length of one complete cycle is called a period. Let us see with the below graph the period of the trigonometric function cos.

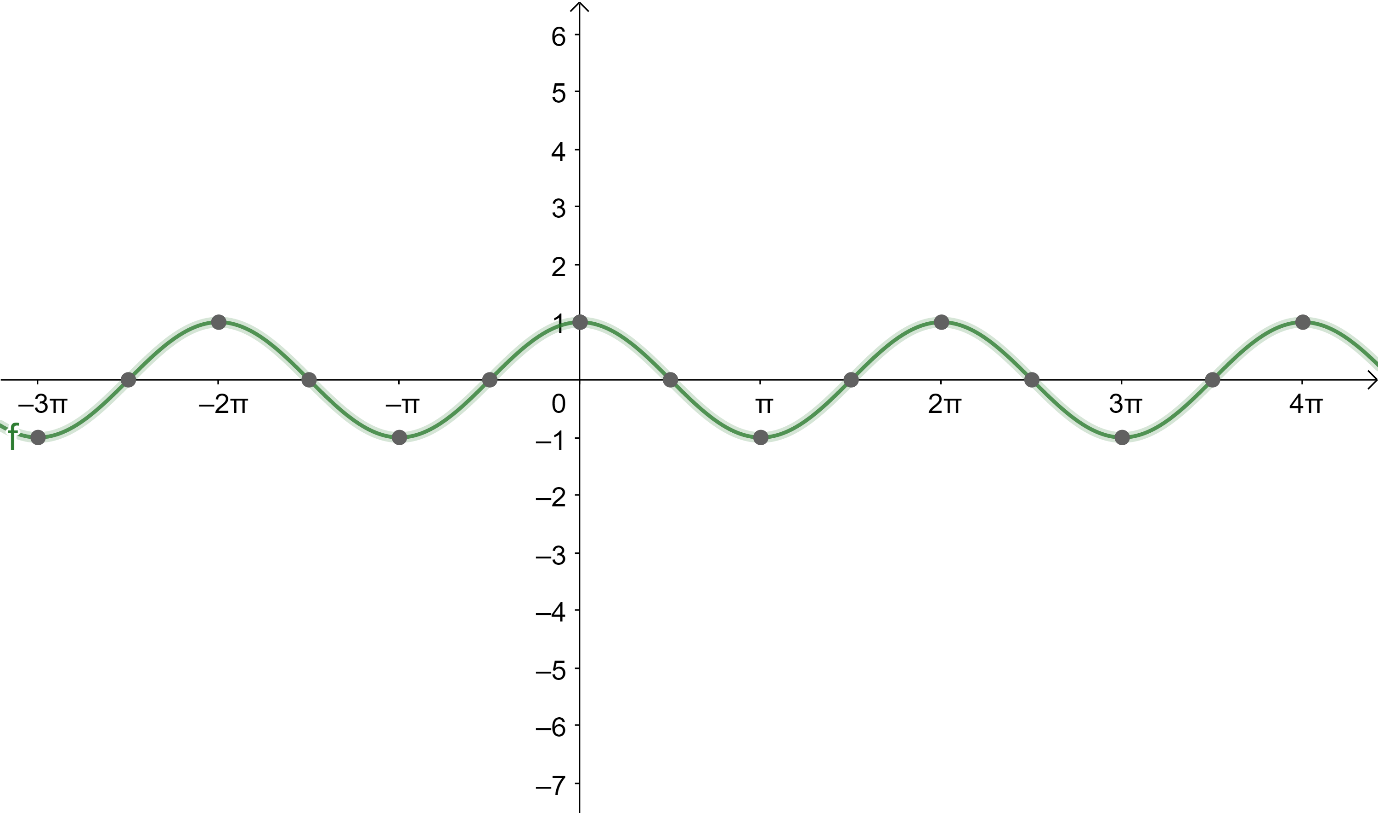
From the above graph we infer that the period for the trigonometric function $\cos x$ is $2\pi$ Consider a function given to us which is $\cos 10t$, on equating the trigonometric $\cos 10t$ to $\cos x$. On showing it mathematically we get:
$\Rightarrow \cos x=\cos 10t$
Since both sides of the trigonometric function $\cos$ are present, so we can equate the angles of the function. On doing this we get:
$\Rightarrow x=10t$
$\Rightarrow \dfrac{x}{10}=t$
The period of the trigonometric function $\cos x$ is $2\pi$. So for the angle $10t$, the period will be:
$\Rightarrow \dfrac{2\pi }{10}$
On dividing both the numerator and the denominator by $5$, we get:
$\Rightarrow \dfrac{\pi }{5}$
$\therefore$ The period of $f\left( t \right)=\cos 10t$.

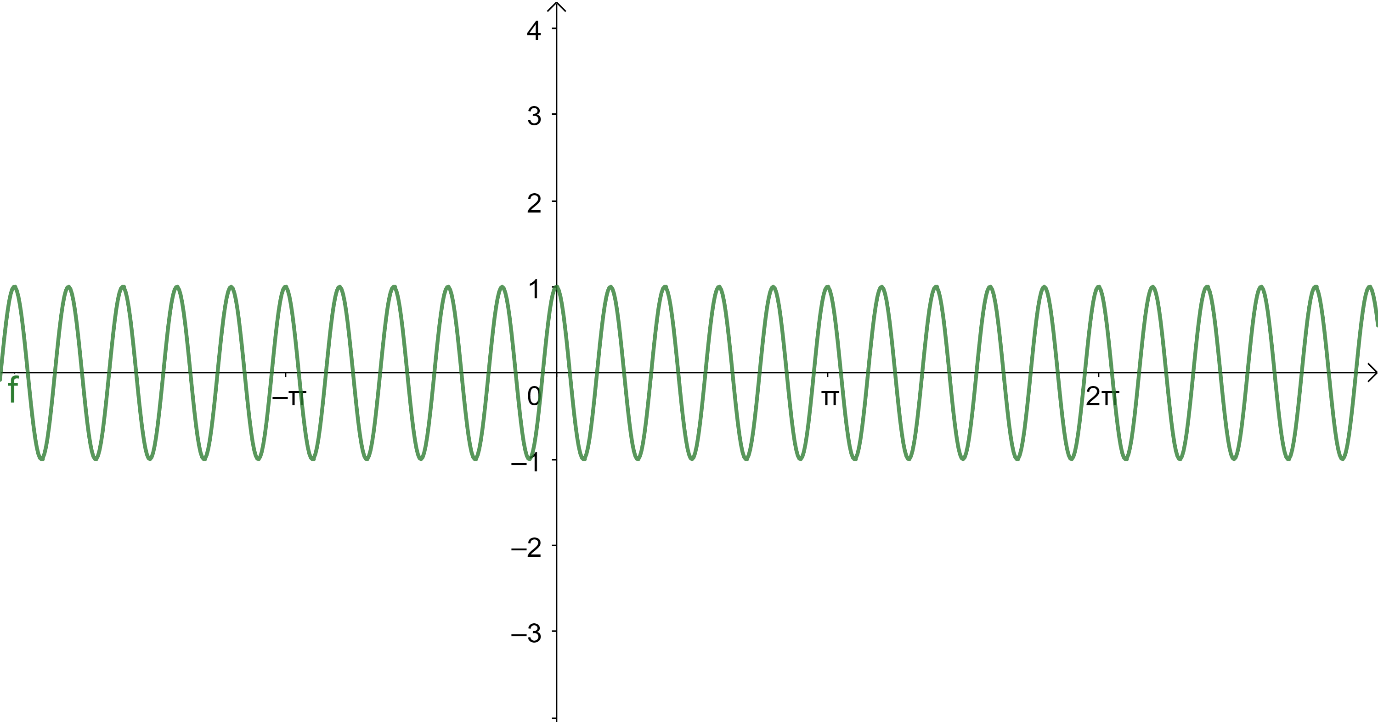
Note: The graph for the function $\cos 10t$ is drawn below which shows that the period of the function is the same as the answer we got $\dfrac{\pi }{5}$.

Periods of all the trigonometric functions should be known to us for solving the problem.