Question

What is the perimeter of a triangle with vertices of $\left( {2,0} \right)$ , $\left( {2, - 3} \right)$ and $\left( { - 2, - 3} \right)$?

Answer 1

First, we need to assume the vertices as A, B, and C. We are asked to find the perimeter of the given triangle. This means that we need to sum all the sides of the triangle. But, we are not given the length of the sides directly. So, we need to find the length of each side. Then we need to sum all the lengths to obtain the required answer.
Formula to be used:
The required formulae to be applied in this problem are as follows.
a) Distance formula:
Length of the side $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
b) Perimeter of a triangle $=$ sum of the length of all sides of the triangle

Complete step by step answer:
Let the given vertices be $A\left( {2,0} \right)$ , $B\left( {2, - 3} \right)$ and $C\left( { - 2, - 3} \right)$
We shall represent the given points using a graph.

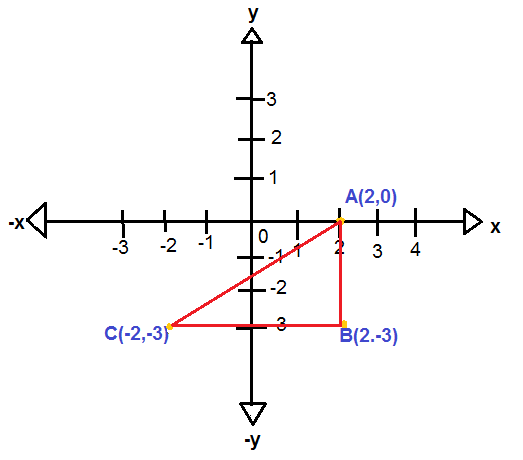
To find the length of the sides, we need to apply the distance formula.
For the length of the side AB, we shall apply the distance formula.
Here $A\left( {2,0} \right)$ and $B\left( {2, - 3} \right)$
Thus, AB $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$= \sqrt {{{\left( {2 - 2} \right)}^2} + {{\left( { - 3 - 0} \right)}^2}}$
$= \sqrt {{0^2} + {{\left( { - 3} \right)}^2}}$
$= \sqrt 9$
$= 3$
Thus AB $= 3$Units
For the length of the side BC, we shall apply the distance formula.
Here $B\left( {2, - 3} \right)$ and $C\left( { - 2, - 3} \right)$
Thus, BC $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$= \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( { - 3 - \left( { - 3} \right)} \right)}^2}}$
$= \sqrt {{{\left( { - 4} \right)}^2} + {{\left( { - 3 + 3} \right)}^2}}$
$= \sqrt {16 + {0^2}}$
$= 4$
Thus BC $= 4$Units
For the length of the side CA, we shall apply the distance formula.
Here $C\left( { - 2, - 3} \right)$ and $A\left( {2,0} \right)$
Thus, CA $= \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$
$= \sqrt {{{\left( {2 - \left( { - 2} \right)} \right)}^2} + {{\left( { - 3 - 0} \right)}^2}}$
$= \sqrt {{{\left( {2 + 2} \right)}^2} + {{\left( { - 3} \right)}^2}}$
$= \sqrt {{4^2} + {{\left( { - 3} \right)}^2}}$
$= \sqrt {16 + 9}$
$= \sqrt {25}$
$= 5$
Thus CA $= 5$Units
Hence, we have AB $= 3$, BC $= 4$ , and CA $= 5$

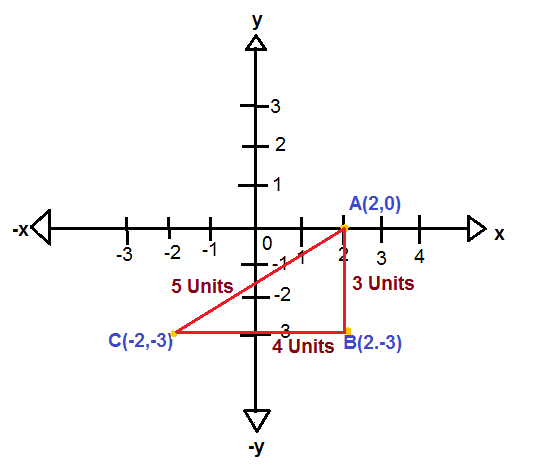
Now, we shall apply the formula to find the perimeter.
Thus, the Perimeter of a triangle $=$ $AB + BC + CA$
$= 3 + 4 + 5$
$= 12$ Units

Note:
Here we are given vertices of the triangle. So we have applied the distance formula to find the length of each side of the triangle and we applied the formula to find the perimeter. If we are given the length directly, we don’t need to apply the distance formula. We need to just apply the formula to find the perimeter.