Question

What is the perimeter of a regular octagon with a radius of length 20?

Answer 1

Hint : Here in this question, we have to find the perimeter of a regular octagon of given radius of length $r = 20$ . First, we have to find the length $l$ of each side of octagon using a distance formula $l = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}}$ and later find a perimeter using a formula $P = 8 \times l\,$ . If we are finding the perimeter of a regular octagon, then we know that all eight sides are equal lengths, so we can simplify the formula using multiplication operation to get the required solution.

Complete step-by-step answer :
In geometry, perimeter can be defined as the path or the boundary that surrounds a shape. It can also be defined as the length of the outline of a shape.
If a octagon is regular, then all the sides are equal in length, and eight angles are of equal measures
Consider a regular octagon having radius of length $r = 20$ , which is same for vertices of pentagons.
In figure, the red circle circumscribes the outer radius and the green circle the inner one.

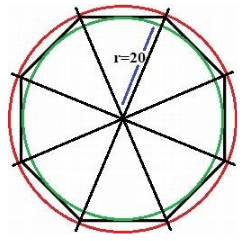
Let consider $r = 20$ be the outer radius - that is the radius of the red circle.
Then, the vertices of the octagon centred at origin i.e., $\left( {0,0} \right)$ are at $\left( { \pm \,r,0} \right)$ , $\left( {0, \pm \,r} \right)$ and $\left( { \pm \,\dfrac{r}{{\sqrt 2 }}, \pm \,\dfrac{r}{{\sqrt 2 }}} \right)$ .
So the length of one side of regular octagon is distance between $\left( {r,\,0} \right)$ and $\left( {\dfrac{r}{{\sqrt 2 }},\,\dfrac{r}{{\sqrt 2 }}} \right)$
Let consider a distance formula $l = \sqrt {{{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{x_2} - {x_1}} \right)}^2}}$ , on substituting we have
$\Rightarrow \,\,l = \sqrt {{{\left( {\dfrac{r}{{\sqrt 2 }} - 0} \right)}^2} + {{\left( {\dfrac{r}{{\sqrt 2 }} - r} \right)}^2}}$
$\Rightarrow \,\,l = \sqrt {{{\left( {\dfrac{r}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{r}{{\sqrt 2 }} - r} \right)}^2}}$
$\Rightarrow \,\,l = \sqrt {{r^2}{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2} + {r^2}{{\left( {\dfrac{1}{{\sqrt 2 }} - 1} \right)}^2}}$
Take ${r^2}$ to outside, then
$\Rightarrow \,\,l = r\sqrt {{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{1}{{\sqrt 2 }} - 1} \right)}^2}}$
Simplify using a algebraic identity ${\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab$ , we have
$\Rightarrow \,\,l = r\sqrt {\dfrac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + \dfrac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} + 1 - \dfrac{2}{{\sqrt 2 }}}$
On simplification, we get
$\Rightarrow \,\,l = r\sqrt {\dfrac{1}{2} + \dfrac{1}{2} + 1 - \dfrac{2}{{\sqrt 2 }}}$
$\Rightarrow \,\,l = r\sqrt {1 + 1 - \dfrac{2}{{\sqrt 2 }}}$
$\Rightarrow \,\,l = r\sqrt {2 - \sqrt 2 }$ ------(1)
Which is the length of the each side of the regular octagon when $r$ be the outer radius.
Then perimeter of regular octagon is
$\Rightarrow \,\,P = 8 \times l\,$
On substituting equation (1), we have
$\Rightarrow \,\,P = 8 \times r\sqrt {2 - \sqrt 2 }$
given $r = 20$ , then
$\Rightarrow \,\,P = 8 \times 20\sqrt {2 - \sqrt 2 }$
$\Rightarrow \,\,P = 160\sqrt {2 - \sqrt 2 }$
On using calculator, we get the exact value
$\Rightarrow \,\,P = 160\sqrt {2 - \sqrt 2 } \simeq 122.46$
Now, consider ${r_1} = 20$ be the inner radius - that is the radius of the green circle
The inner radius will be ${r_1} = r\cos \theta$
From the figure we have $\theta = \dfrac{\pi }{8}$ , then
$\Rightarrow \,\,{r_1} = r\cos \left( {\dfrac{\pi }{8}} \right)$
By using a calculator, the value of $\cos \left( {\dfrac{\pi }{8}} \right) = \dfrac{{\sqrt {2 + \sqrt 2 } }}{2}$ , then
$\Rightarrow \,\,{r_1} = r\left( {\dfrac{{\sqrt {2 + \sqrt 2 } }}{2}} \right)$
On cross multiplication, we have
$\Rightarrow \,r = \,\dfrac{{2{r_1}}}{{\sqrt {2 + \sqrt 2 } }}$ ------(2)
On substituting equation (2) in (1), we get the length of each side i.e.,
$\Rightarrow \,\,l = \dfrac{{2{r_1}}}{{\sqrt {2 + \sqrt 2 } }}\sqrt {2 - \sqrt 2 }$
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {2 - \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }}$
To rationalize the denominator, we have to multiply and divide the RHS by $\sqrt {2 + \sqrt 2 }$ , then
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {2 - \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }} \times \dfrac{{\sqrt {2 + \sqrt 2 } }}{{\sqrt {2 + \sqrt 2 } }}$
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\left( {\sqrt {2 - \sqrt 2 } } \right)\left( {\sqrt {2 + \sqrt 2 } } \right)}}{{\left( {\sqrt {2 + \sqrt 2 } } \right)\left( {\sqrt {2 + \sqrt 2 } } \right)}}$
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {\left( {2 - \sqrt 2 } \right)\left( {2 + \sqrt 2 } \right)} }}{{{{\left( {\sqrt {2 + \sqrt 2 } } \right)}^2}}}$
On simplification, we get
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt {4 + 2\sqrt 2 - 2\sqrt 2 - 2} }}{{2 + \sqrt 2 }}$
$\Rightarrow \,\,l = 2{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}$ -----------(3)
Which is the length of each side of the regular octagon when $r$ be the inner radius.
Then perimeter of regular octagon is
$\Rightarrow \,\,P = 8 \times l\,$
On substituting equation (1), we have
$\Rightarrow \,\,P = 8 \times 2{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}$
$\Rightarrow \,\,P = 16{r_1}\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}$
given ${r_1} = 20$ , then
$\Rightarrow \,\,P = 16\left( {20} \right)\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}$
$\Rightarrow \,\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }}$
On using calculator, we get the exact value
$\Rightarrow \,\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }} \simeq 132.55$
Hence, the perimeter of regular octagon of radius 20 is
If the outer radius is 20, then the perimeter is: $P = 160\sqrt {2 - \sqrt 2 } \simeq 122.46$
If the inner radius is 20, then the perimeter is: $\,P = 320\dfrac{{\sqrt 2 }}{{2 + \sqrt 2 }} \simeq 132.55$
So, the correct answer is “$\simeq 132.55$”.

Note : While determining the perimeter we use the formula. The unit for the perimeter will be the same as the unit of the length of a side or polygon. Whereas the unit for the area will be the square of the unit of the length of a polygon. We should not forget to write the unit with a final answer and we should also know about regular and irregular polygons.