Question

What is the parallax formula and how is it used to calculate the distance between two stars?

Answer 1

In order to solve this question, we are going to firstly define the parallax formula then starting off with how it is used to measure the distance between any two points, the parallax is used to measure the distance between the two stars which is shown by deriving the formula for distance.

Formula used: The distance between the two stars is equal to:
$d = \dfrac{1}{p}$
Where $p$ is the parallax angle

Complete step by step answer:
According to the parallax formula, the distance between the two stars is equal to $1$ divided by the parallax angle, $p$, where $p$ is measured in seconds and $d$ in parsecs.
$d = \dfrac{1}{p}$
The distance between the two stars is very large as compared to any two objects that are present on earth’s surface. If we observe the one star from two points on the earth’s surface diametrically opposite to each other. Then, we would have a separation of about $2AU$. Now, this is enough to get a noticeable angle,$\alpha$ between the stars is two different apparent positions. Considering the figure below.

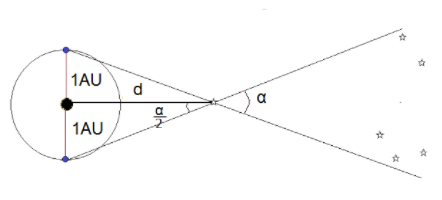
By cutting α in half, we get a right triangle where one leg is the distance between the sun and the other star. Let us consider that $\dfrac{\alpha }{2} = p$
The tangent of this angle can be used to measure the distance between the stars.
$\tan \alpha = \dfrac{{1AU}}{d}$
Since the star is very far away so the angle is very small and hence the tangent is also very small.
$p = \dfrac{{1AU}}{d}$
Thus, the distance is calculated as
$d = \dfrac{{1AU}}{p}$

Note: It is important to note that the Parallax is a method of using two observation points to measure its distance to an object by observing how it appears to move against a background. One way to understand parallax is to look at a nearby object and note its position against a wall. If you look with just one eye, then the other, the object appears to move against the background.