Question

What is the output of the given logic gate?

$\left. A \right)A\centerdot B$
$\left. B \right)\overline{A}\centerdot \overline{B}$
$\left. C \right)\overline{A}+\overline{B}$
$\left. D \right)A+B$

Answer 1

A NAND gate is a combination of an AND gate and a NOT gate. An AND gate provides an output of 1 only if all the inputs are 1 whereas a NOT gate provides an output, which is nothing but the opposite of the input. The output of a NAND gate can easily be determined from this combination of AND gate and a NOT gate. Here, in this question, we proceed by using de Morgan’s first theorem. Also, it is clear that A and B are the inputs of the NAND gate, which can be written as:
$A=\overline{\overline{A}};B=\overline{\overline{B}}$
Formula used:
From de Morgan's first theorem we have,
$\overline{A\centerdot B}=\overline{A}+\overline{B}$

Complete answer:
De Morgan’s First theorem proves that when two (or more) input variables are connected using an AND gate, they are equivalent to the OR of the complements of the individual variables. Thus, the equivalent of the NAND function will be a negative-OR function, proving that
$\overline{A\centerdot B}=\overline{A}+\overline{B}$
If we multiply a binary digit with itself the result is also the same as the initial binary digit.
For example, 1 is a binary digit and if we are multiplying 1 with itself, we get 1 itself as the output.
In the same way, if $A$ is the binary digit or binary input the multiplication of $A$ with itself is also $A$ .
i.e. $A\centerdot A=A$

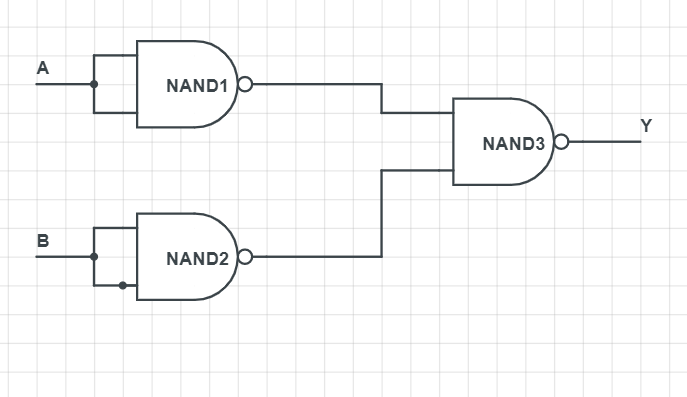
The double complement of a binary digit is also the same with the initial binary digit.
For example, 1 is a binary digit then $\overline{\overline{1}}=\overline{0}=1$
In the same way A is a binary digit then $\overline{\overline{A}}=A$
For the first NAND gate both the inputs are A. So the inputs are $A=A;B=A$
The output of the first NAND gate is ${{Y}_{1}}=\overline{A\centerdot A}=\overline{A}\to \left( 1 \right)$
In the same way for the second NAND gate both the inputs are B. So the inputs are $A=B;B=B$
The output of the second NAND gate is ${{Y}_{2}}=\overline{B\centerdot B}=\overline{B}\to \left( 2 \right)$
Now the inputs of the third NAND gate is $A={{Y}_{1}};B={{Y}_{2}}$
The output of the third NAND gate is $Y=\overline{{{Y}_{1}}\centerdot {{Y}_{2}}}$
Substituting the values from equation $\left( 1 \right)$ and $\left( 2 \right)$ in the above equation we get,
$Y=\overline{\overline{A}\centerdot \overline{B}}$
By applying the De Morgan's theorem, we can get
$Y=\overline{\overline{A}}+\overline{\overline{B}}=A+B$
The output of the combination is $Y=A+B$ .

Therefore, option D is the correct answer and clearly, this combination represents a OR gate.

Additional information:
NAND gates and NOR gates are also called as universal logic gates. By using these gates, we can construct any one of the basic logic gates.

Note: While solving the problems on logic gates, first we have to find the output of each gate and we have to apply the equations of De Morgan's theorem if necessary. This problem can also be solved by assigning values to inputs $A$ and$B$, and then, applying the logic of a NAND gate. In this method, four combinations are there to solve.