Question

What is the orthocentre of a triangle with corners at $\left( {3,1} \right),\left( {4,5} \right)$ and $\left( {2,2} \right)$ ?

Answer 1

To solve this problem, we should know that the orthocentre is the point of intersection of the triangles three altitudes. Here, we will first let the coordinate of the orthocentre be $\left( {x,y} \right)$ Then we will use the given points to find the slope of the sides. Then we will find the slope of the corresponding perpendicular lines. Then we will use slope and the corresponding vertex and substitute them in the slope point form to find the equation of the altitudes. After that we will simplify both the equations and find the values of $x$ and $y$ Hence, we will get the required result.

Formulas used:
Slope, $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
Slope of perpendicular line is $\dfrac{{ - 1}}{m}$
Slope point form, $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$

Complete step-by-step answer:
Let the given points be $A\left( {3,1} \right),B\left( {4,5} \right)$ and $C\left( {2,2} \right)$
Here we have to find the orthocentre.
So, let the coordinate of orthocentre be $\left( {x,y} \right)$
Now first of all, we will draw a rough diagram with the given three points

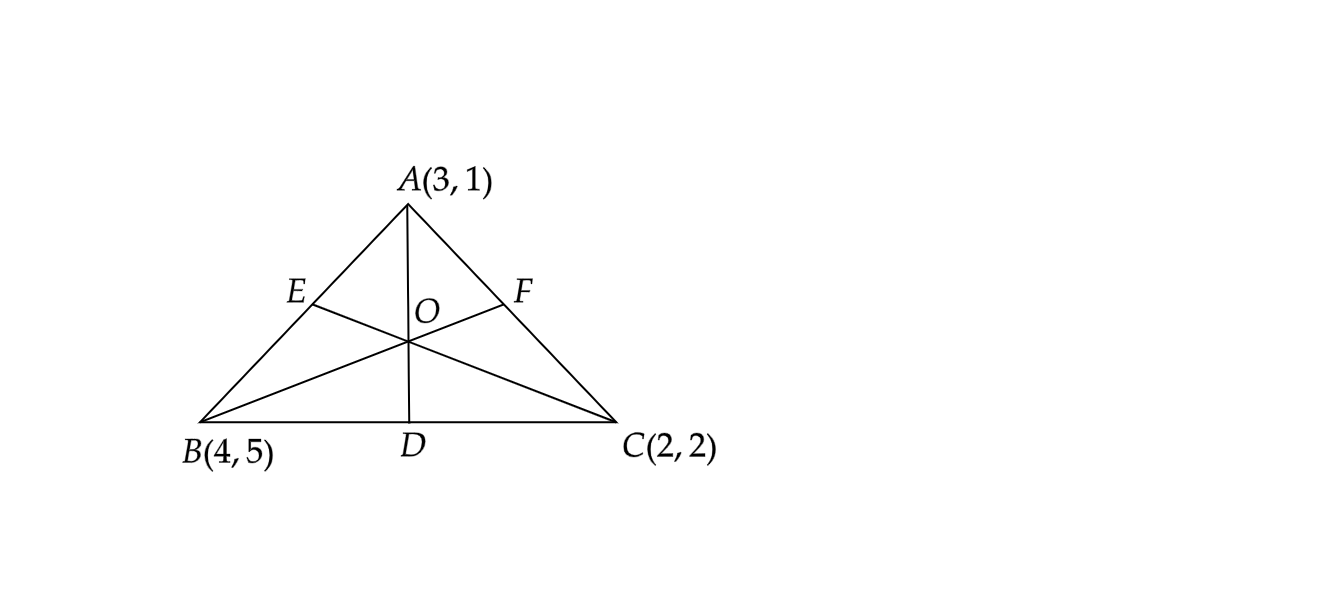
Now we will find the slopes
We know that
Slope, $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
So, now the slope of $AB$ with the points $A\left( {3,1} \right),B\left( {4,5} \right)$ will be
${m_{AB}} = \dfrac{{5 - 1}}{{4 - 3}} = \dfrac{4}{1}$
Now as we can see, $CE$ is perpendicular to $AB$
And we know that
Slope of perpendicular line is $\dfrac{{ - 1}}{m}$
Therefore, slope of $CE$ is $\dfrac{{ - 1}}{{{m_{AB}}}}$
$\Rightarrow {m_{CE}} = \dfrac{{ - 1}}{4}$
Now we will find the slope of $BC$ with the points $B\left( {4,5} \right),C\left( {2,2} \right)$
So, the slope of $BC$ will be
${m_{BC}} = \dfrac{{2 - 4}}{{2 - 5}} = \dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3}$
Now as we can see, $AD$ is perpendicular to $BC$
Therefore, slope of $AD$ is $\dfrac{{ - 1}}{{{m_{BC}}}}$
$\Rightarrow {m_{AD}} = \dfrac{{ - 1}}{{\dfrac{2}{3}}} = \dfrac{{ - 3}}{2}$
Now we will find the equation of the perpendicular lines
According to the slope point form,
$\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$
Therefore, the equation of $CE$ whose point is $\left( {2,2} \right)$ and slope is $\dfrac{{ - 1}}{4}$ will be
$\Rightarrow y - 2 = \dfrac{{ - 1}}{4}\left( {x - 2} \right)$
On solving, we get
$\Rightarrow 4y - 8 = - x + 2$
$\Rightarrow x + 4y = 10{\text{ }} - - - \left( i \right)$
And the equation of $AD$ whose point is $\left( {3,1} \right)$ and slope is $\dfrac{{ - 3}}{2}$ will be
$\Rightarrow y - 1 = \dfrac{{ - 3}}{2}\left( {x - 3} \right)$
On solving, we get
$\Rightarrow 2y - 2 = - 3x + 9$
$\Rightarrow 3x + 2y = 11{\text{ }} - - - \left( {ii} \right)$
Now we will solve equation $\left( i \right)$ and $\left( {ii} \right)$
Multiply equation $\left( i \right)$ by $3$ and subtract both the equations,
$\Rightarrow 3x + 12y - 3x - 2y = 30 - 11$
$\Rightarrow 10y = 19$
$\Rightarrow y = \dfrac{{19}}{{10}}$
Now on substituting the value of $y$ in equation $\left( i \right)$ we get
$x + 4\left( {\dfrac{{19}}{{10}}} \right) = 10$
$\Rightarrow x = 10 - \dfrac{{76}}{{10}}$
$\Rightarrow x = \dfrac{{24}}{{10}}$
Hence, the coordinates of orthocentre $O\left( {x,y} \right)$ is $\left( {\dfrac{{24}}{{10}},\dfrac{{19}}{{10}}} \right)$

Note: While solving these types of problems, we should always remember that we can find the slopes if we have two coordinates. We can find an equation, if we have a slope and a point using the slope point form. And also, we should know that the slope of the perpendicular line is negative or reciprocal of the slope of the given line. Also, while finding slope of the perpendicular line, always consider the corresponding slope and a point. As another point or slope can cause errors for the further calculations. So, be careful while solving the problem.