Question

What is the ordered pair that satisfies the equation $3x + 4y = 24$?

Answer 1

We know that a first degree equation in x and y, $ax + by + c = 0$ always represents a straight line. This form is known as the general form of straight line.
Formula used: From the general form of straight line, $ax + by + c = 0$, we know that

Slope of this line $= - \dfrac{a}{b} = - \dfrac{{coeff.of(x)}}{{coeff.of(y)}}$
Intercept by this line on x-axis$= - \dfrac{c}{a}$
Intercept by this line on y-axis$= - \dfrac{c}{b}$
Given: Equation $3x + 4y = 24$
To find: Ordered pair that satisfy the given equation, $3x + 4y = 24$

Complete step-by-step solution:
Step 1: Conversion of given equation into its general form of equation
We know that the general form of straight line is given by the equation,
$ax + by + c = 0$
Now, rearranging the terms of the given equation $3x + 4y = 24$,
Taking $24$on the left hand side of the equation, we get
\Rightarrow $$$$3x + 4y = 24
\Rightarrow $$$$3x + 4y - 24 = 0 (Given equation is now converted into general form of straight line)
Step 2: comparing equations $3x + 4y = 24$& $ax + by + c = 0$ both, we get
\Rightarrow $$$$ax + by + c = 0
\Rightarrow $$$$3x + 4y = 24
\Leftrightarrow $$$$a = 3,b = 4\& c = - 24
Step 3: Finding the ordered pair that satisfy the given equation,
Now, from general form of straight line i.e. $ax + by + c = 0$, we know that

1. Intercept by this line on x-axis $= - \dfrac{c}{a}$
   Substituting the values of a & c we get,
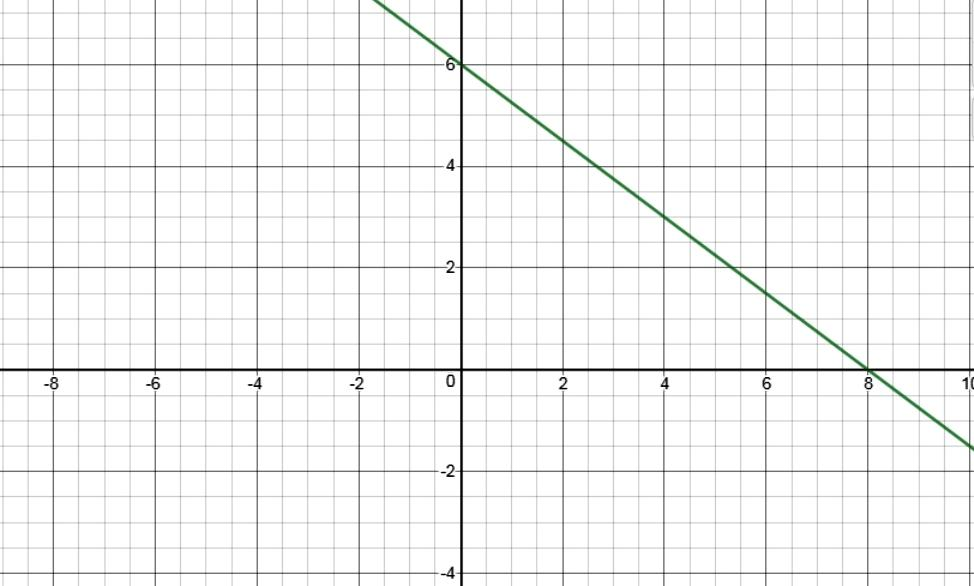
   Intercept by this line on x-axis $= - \dfrac{{( - 24)}}{3} = 8$& since this intercept is only on x-axis therefore, $y = 0$
   So, $(8,0)$is a point that satisfy the equation $3x + 4y = 24$
2. Intercept by this line on y-axis$= - \dfrac{c}{b}$
   Substituting the values of b & c we get,
   Intercept by this line on y-axis $= - \dfrac{{( - 24)}}{4} = 6$& since this intercept is only on y-axis therefore, $x = 0$
   So, $(0,6)$ is a point that satisfy the equation $3x + 4y = 24$
   Hence, $(8,0)$ &$(0,6)$are the ordered pairs that satisfies the equation $3x + 4y = 24$.
   

Note: Here we need to remember few important properties of straight line.

Equation of line parallel to line $ax + by + c = 0$ is, $ax + by + \lambda = 0$
Equation of line perpendicular to line $ax + by + c = 0$ is, $bx - ay + k = 0$
Here $\lambda$, $k$ are parameters and their values are obtained with the help of additional information given in the problem.