Question

What is the number of points on the line 3x + 4y = 5, which are at a distance of ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta ,\theta \in R$ from the point (1, 3)?
(a). 1
(b). 2
(c). 3
(d). Infinite

Answer 1

Hint: Find the shortest distance of the point (1, 3) from the line 3x + 4y = 5 using the formula $\dfrac{{|a{x_0} + b{y_0} + c|}}{{\sqrt {{a^2} + {b^2}} }}$. Then find if the distance ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta ,\theta \in R$ is smaller than, equal to, or greater than this distance and conclude the answer.

Complete step-by-step answer:
We need to find the number of points on the line 3x + 4y = 5, which are at a distance of ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta ,\theta \in R$ from the point (1, 3).
For this, we first find the shortest distance between the point (1, 3) and 3x + 4y = 5.

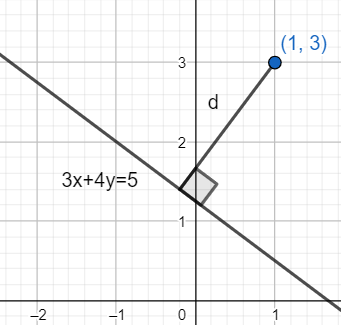
The shortest distance of a point $({x_0},{y_0})$ from a line $ax + by + c = 0$ is given as follows:
$d = \dfrac{{|a{x_0} + b{y_0} + c|}}{{\sqrt {{a^2} + {b^2}} }}$
The standard form of the line 3x +4y = 5 is given as follows:
$3x + 4y - 5 = 0$
Now, the distance of the point (1, 3) from this line is given as follows:
$d = \dfrac{{|3(1) + 4(3) - 5|}}{{\sqrt {{3^2} + {4^2}} }}$
Simplifying, we have:
$d = \dfrac{{|3 + 12 - 5|}}{{\sqrt {9 + 16} }}$
$d = \dfrac{{|10|}}{{\sqrt {25} }}$
$d = \dfrac{{10}}{5}$
$d = 2..............(1)$
Now, we find the value of ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta$.
We know that ${\sec ^2}\theta = 1 + {\tan ^2}\theta$ and also, we know that ${\text{cose}}{{\text{c}}^2}\theta = 1 + {\cot ^2}\theta$, hence, we have:
${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta = 1 + {\tan ^2}\theta + 2(1 + {\cot ^2}\theta )$
Simplifying, we have:
${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta = 1 + {\tan ^2}\theta + 2 + 2{\cot ^2}\theta$
${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta = 3 + {\tan ^2}\theta + 2{\cot ^2}\theta$
The squares of tangent and cotangent functions are positive and hence, we have:
${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta \geqslant 3$
Hence, we observe that the distance of ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta$ is greater than the shortest distance between the point (1, 3) and the line 3x + 4y = 5, hence, there are two points on either side of the shortest distance, that equals the distance of ${\sec ^2}\theta + 2{\text{cose}}{{\text{c}}^2}\theta$.
Hence, the correct answer is option (b).

Note: You can also express the point on the line 3x + 4y = 5 as $\left( {x,\dfrac{{5 - 3x}}{4}} \right)$ and equate the distance between two points as $\sqrt {{{({x_1},{y_1})}^2} + {{({y_2} - {y_1})}^2}}$ to find the number of values of x.