Question

What is the number of atoms (z) in a simple cubic unit cell?

Answer 1

Hint : In a simple cubic unit cell, atoms are present only at the corners of the cube. Using this information, and the contribution of each atom to that particular unit cell, we can calculate the number of atoms in a simple cubic unit cell. A primitive or simple unit cell has motifs at the corners of the unit cell, except for in the case of a trigonal unit cell. Each crystal system has a primitive unit cell. Thus, there are a total of $7$ primitive unit cells.

Complete Step By Step Answer:
The three Bravais lattices belonging to the cubic system are simple (P), body-centred (I) and face-centred (F).
The simple cubic unit cell can be depicted as follows:

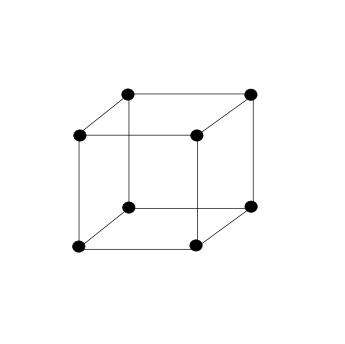
As shown in the picture, there are atoms only at the corners of the unit cell. A cube has $8$ corners. Hence, in a simple cubic lattice, atoms are present only at the eight corners of the cube. The contribution of each atom at the corner towards the unit cell is $\dfrac{1}{8}$ since it is shared by $8$ unit cells. Therefore,
${\text{Contribution by 8 atoms present at corners}}\,\, = \,\,\dfrac{1}{8} \times 8 = 1 \\\ {\text{That is, }}z = 1 \\\$
Hence, the number of atoms (z) present in a simple cubic unit cell is $1$ .

Note :
In a body-centred cubic unit cell, there atoms at the $8$ corners as well at the centre of the cube. Hence, it has $z\, = \,2$ . For face-centred cubic unit cells, atoms are present at the $8$ corners as well as at the centres of each face. Hence, $z\, = \,4$ .