Question

What is the number of atoms in the unit cell of the body centred cubic crystal?
(A) 1
(B) 3
(C) 4
(D) 2

Answer 1

In a body-centred cubic structure atoms are present at every corner of the unit cell and at the body centre. Now check the contribution of each atom to the unit cell and then calculate the total number of atoms present in a bcc lattice by adding the contribution of all the corner atoms and the atom present at the body centre.

Complete step by step solution:
-So, first of all, let us discuss closed packed structures. We should know that the closed packed structure refers to the most tightly packed structure. We should know that the unit cell is the most basic and it occupies very least volume and it is the repeating structure of any solid. We should know that we assume atoms as spherical. This explains the bonding and structures of metallic crystals. These spherical particles can be packed into different arrangements. In closest packed structures, the arrangements of the spheres are densely packed in order to take up the greatest amount of space possible.
-Now, we will calculate the number of atoms in each type of unit cell.
-First, we will take a simple cubic unit cell. We should know that 8 atoms are located on 8 corners of the lattice. Each atom contributes $\left( {\dfrac{1}{8}} \right)$ of the original volume of the cell. So, we can say that: $8 \times \dfrac{1}{8}$ = 1 atom
There is one atom in a simple cubic unit cell.
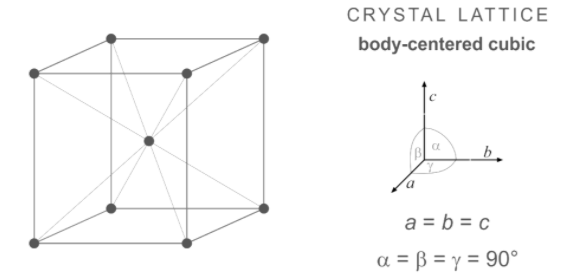
-In the same way, we will calculate atoms for body-centred cubic. There are 8 corners and 1 corner shares 1/8th the volume of the entire cell, so: $8 \times \dfrac{1}{8}$ = 1 atom
There is also 1 atom at the centre of the body of the cube. This can’t be shared. So, it will stay as one atom whole: 1 × 1 = 1 atom
Total atoms = 1 + 1 = 2 atoms
So, from this, we can say that the number of atoms in the unit cell of the body-centred cubic crystal is 2.

Hence, option D is correct.

Additional information:
The structure of body-centred cubic is represented below:

Note: We should know that the BCC structure consisting of higher densities is very common in nature. The examples having BCC structure are iron, chromium, tungsten, and niobium. We should know that multi-element compounds often have crystal structures based on a cubic crystal system. The examples of multi-element compounds having BCC systems are caesium chloride, high-temp RbCl, AlCo, AgZn, etc.