Question

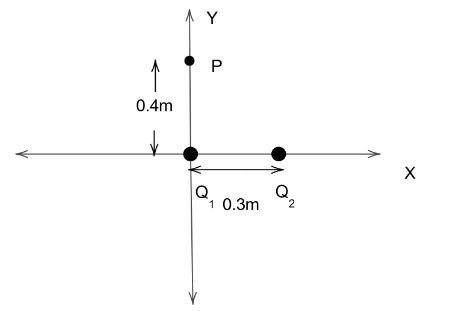
What is the net electric field? Given that ${Q_1} = 7 \times {10^{ - 6}}$ is located at the origin and ${Q_2} = 5 \times {10^{ - 6}}$ is located $0.3\,m$ to the right of ${Q_1}$ what is the net electric field at a point $P$ located $0.4\,m$ above ${Q_1}$?

Answer 1

We are asked about the net electric field at a given point. We can start to attempt this question by drawing a suitable diagram. We can then find the net electric field by finding the electric field due to the charges individually and then adding them according to the laws of vector addition.

Formulas used:
The formula used to find the electric field at a point is given by,
$E = k\dfrac{Q}{{{r^2}}}$
Where $Q$ is the charge and $r$ is the distance between the point and the charge.
$k = 9 \times {10^9}Nm/{C^2}$
The electric field is also found using the formula,
$E = \sqrt {{E_x}^2 + {E_y}^2}$
Where ${E_x}$ and ${E_y}$ are the $x$ and $y$ components respectively

Complete step by step answer:
Let us start by drawing a diagram for the data given in the question

Now that we have drawn a suitable diagram, let us move onto finding the electric field due to the first charge at point P using the formula $E = k\dfrac{Q}{r}$. Substituting we get,

\Rightarrow {E_1} = 9 \times {10^9} \times \dfrac{{7 \times {{10}^{ - 6}}}}{{0.4 \times 0.4}} \\\ \Rightarrow {E_1} = 3.93 \times {10^5}N/C$$ Now we can move onto finding the electric field due to the second charge. In order to find this, let us consider a right angles triangle as shown in the figure,  From this we can find the distance between the second charge and the point using the Pythagoras theorem, $$P{Q_2} = \sqrt {{{0.3}^2} + {{0.4}^2}} = 0.5$$ Now that we have found the distance between the point and the charge, we can move onto finding the electric field due to the second charge at the given point P using the formula, $$E = k\dfrac{Q}{{{r^2}}}$$ Substituting the values, we get $${E_2} = k\dfrac{{{Q_2}}}{{{r^2}}} \\\ \Rightarrow {E_2} = 9 \times {10^9} \times \dfrac{{5 \times {{10}^{ - 6}}}}{{0.5 \times 0.5}} \\\ \Rightarrow {E_2} = 1.79 \times {10^7}N/C$$ We will now split this into two components, the x and y components as it is inclined at an angle. This angle can be found using the formula to find the slope of the line joining P and the second charge $$\tan \theta = \dfrac{y}{x}$$ $$\Rightarrow \theta = {\tan ^{ - 1}}\dfrac{y}{x} \\\ \Rightarrow {\tan ^{ - 1}}\dfrac{{0.4}}{{0.3}} = 53.12^\circ $$ We can move onto finding the x and y components of the electric field due to the second charge  The $x$ component will be, $${\left( {{E_2}} \right)_x} = {E_2}\cos \theta \\\ \Rightarrow {\left( {{E_2}} \right)_x} = 1.79 \times {10^7} \times \cos 53.12 \\\ \Rightarrow {\left( {{E_2}} \right)_x} = 1.07 \times {10^7}N/C$$ The y component will be $${\left( {{E_2}} \right)_y} = {E_2}\sin \theta \\\ \Rightarrow {\left( {{E_2}} \right)_y} = 1.79 \times {10^7}\sin 53.12 \\\ \Rightarrow {\left( {{E_2}} \right)_y} = 1.44 \times {10^7}N/C$$ The total or the net electric field can be found using the formula, $${E_{net}} = \sqrt {{{\left( {{E_2}} \right)}_x}^2 + {{\left( {{{\left( {{E_2}} \right)}_y} + {E_1}} \right)}^2}} $$ We add the value of the electric field of the fist charge to the $y$ component because you can see that in the figure, the electric field due to the first charge is in the $y$ direction.Substituting, we get $${E_{net}} = \sqrt {{{\left( {{E_2}} \right)}_x}^2 + {{\left( {{{\left( {{E_2}} \right)}_y} + {E_1}} \right)}^2}} \\\ \Rightarrow {E_{net}} =\sqrt {{{\left( {1.07 \times {{10}^7}} \right)}^2} + {{\left( {1.44 \times {{10}^7} + 3.93 \times {{10}^5}} \right)}^2}} \\\ \therefore {E_{net}} = 1.83 \times {10^7}\,N/C$$ **Therefore, the net electric field is $1.83 \times {10^7}\,N/C$.** **Note:** We can see that the electric field due to the first charge on the point $P$ is in the $y$ direction. We add this value to the $y$ component of the electric field due to the second charge because of this reason. Then we can find the value of the electric field using the vector addition formula.