Question

What is the nature of the graph: $y = - 4{x^2} + 6$
A. Parabola not passing through origin
B. Hyperbola not passing through origin
C. Ellipse not passing through origin
D. It is not a conic.

Answer 1

To find the nature of the graph $y = - 4{x^2} + 6$, let us first draw the graph for different values of $x$. From the graph we can clearly observe the nature of $y = - 4{x^2} + 6$. The given function will be a parabola if it is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. The function will be a hyperbola if it is an open curve with two unconnected branches and has two axes of symmetry. $y = - 4{x^2} + 6$ will be an ellipse if it is a planar curve that has two focal points and appears to be somewhat like a circle.

Complete step by step answer:
We need to find the nature of the graph $y = - 4{x^2} + 6$. Let us first draw this graph. For this, first let us find the coordinates to plot the graph. The table below shows the values of $y = - 4{x^2} + 6$ for different values of $x$.

$x$	$y = - 4{x^2} + 6$
$- 1$	$2$
$0$	$6$
$1$	$2$

From the graph, we can infer that the shape is a U-shape and it extends to infinity. It does not have two axes of symmetry or like a circle. Hence, the given function is a parabola. Now, let us see whether it passes through the origin or not. We know that at the origin $x$ and $y$ coordinates are $0$. That is, the point $\left( {0,0} \right)$. From the graph, we can see that the parabola passes through the point $\left( {0,6} \right)$ not through the origin.Hence, $y = - 4{x^2} + 6$ is a parabola not passing through the origin.

Therefore, the correct option is A.

Note: Do not get confused with parabola and hyperbola. A hyperbola will have the equation of the form $\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1$. The graph of this will be like:

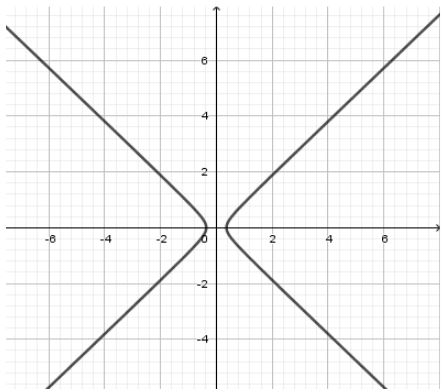
Also, remember that when either $x$ or $y$ is squared but not both, the given equation will be an equation of parabola. When $x$ and $y$ are both squared and the coefficients are positive but different, then the given equation is the equation of ellipse. When $x$ and $y$ are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive, then it resembles a hyperbola.