Question

What is the nature of the graph: $y = 4\left( {1 - {e^{ - 2x}}} \right)$
A. Exponentially increasing graph
B. Exponentially decreasing graph
C. Decreasing graph
D. None of these

Answer 1

Here we have to find whether the given graph is exponentially increasing or decreasing or is it a decreasing graph. So we will use the help of derivatives. Firstly we will find the derivative of the function given with respect to $x$ and then we will check whether the value of derivative is increasing or decreasing for all value of $x \in R$

Complete step-by-step solution:
The exponential function is given as below:
$y = 4\left( {1 - {e^{ - 2x}}} \right)$
The graph of the function can be drawn as follows:

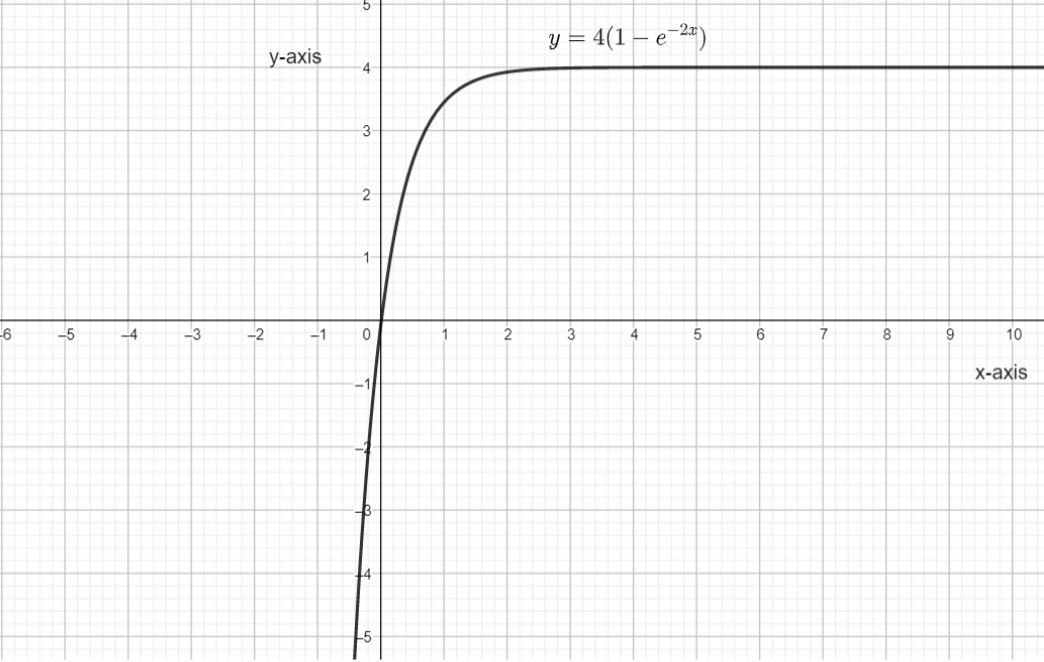
So for finding whether the graph is increasing or decreasing we will firstly find the derivative of the function with respect to $x$ as follows:
$\dfrac{{dy}}{{dx}} = 4\left( {\dfrac{{d\left( 1 \right)}}{{dx}} - \dfrac{{d\left( {{e^{ - 2x}}} \right)}}{{dx}}} \right)$
We know that differentiation of a constant term is $0$ and differentiation of an exponential term is calculated as follows:
$\dfrac{{d\left( {{e^{ax}}} \right)}}{{dx}} = a{e^{ax}}$
Where $a \in R$
So we get,
$\dfrac{{dy}}{{dx}} = 4\left( {0 - \left( { - 2} \right){e^{ - 2x}}} \right)$
$\Rightarrow \dfrac{{dy}}{{dx}} = 8{e^{ - 2x}}$
So as we can see that for any $x \in R$
$\dfrac{{dy}}{{dx}} = 8{e^{ - 2x}} > 0$
So the function is exponentially increasing.
Hence option (A) is correct.

Note: The general form exponential function is $f\left( x \right) = {b^x}$ where $x$ is the exponent and $b$ is any positive number greater than $1$ or we can say that exponential functions are those functions which are in the form of $f\left( x \right) = {e^x}$ where $e$ is a Euler’s number and its value lies between $2\& 3$ and $x$ is the independent variable. The exponential function $f\left( x \right) = {e^x}$ is also known as a natural exponential function. The exponential function can either describe a growth or decay depending upon the independent variable and the graph of the function. In exponential growth the graph increases very slowly at first and then rapidly. In exponential decay the graph decreases rapidly at first and then slowly.