Question

What is the nature of the graph $y=2{{x}^{2}}$ .
A. Parabola passing through the origin
B. Hyperbola passing through the origin
C. Ellipse passing through the origin
D. Hyperbola but not passing through the origin

Answer 1

To find the nature of the graph $y=2{{x}^{2}}$ , let us first draw the graph for different values of x. From the graph we can clearly observe the nature of $y=2{{x}^{2}}$ . The given function will be a parabola if it is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. The function will be a hyperbola if it is an open curve with two unconnected branches and has two axes of symmetry. $y=2{{x}^{2}}$ will be an ellipse if it is a planar curve that has two focal points and appears to be somewhat like a circle.

Complete step by step answer:
We need to find the nature of the graph $y=2{{x}^{2}}$ .
Let us first draw this graph. For this, first let us find the coordinates to plot the graph.
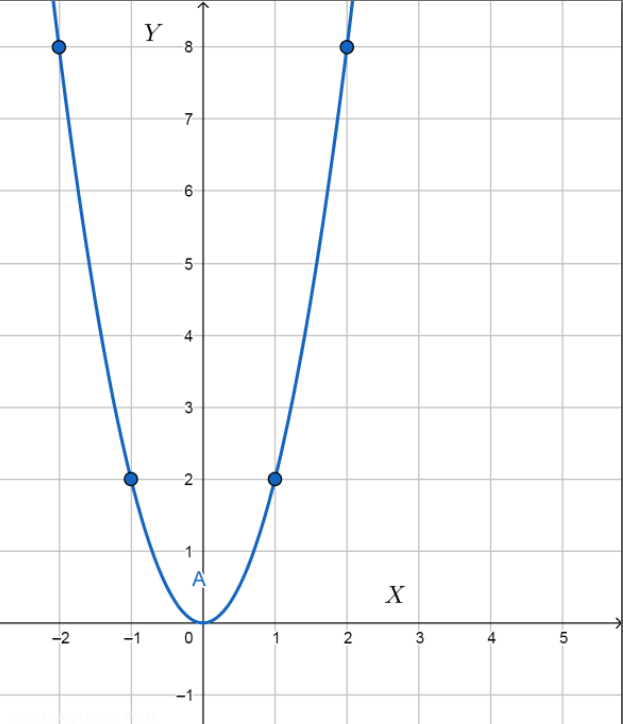
The table below shows the values of $y=2{{x}^{2}}$ for different values of x.

x	$y=2{{x}^{2}}$
-2	8
-1	2
0	0
1	2
2	8

The given options include parabola and hyperbola. Let us see what parabola, hyperbola and ellipse are.
A parabola is a plane curve which is mirror-symmetrical with a single open curve that extends till infinity and is U-shaped. A hyperbola is an open curve with two unconnected branches and has two axes of symmetry. An ellipse is a planar curve that has two focal points and appears to be somewhat like a circle.
From the graph, we can infer that the shape is a U-shape and it extends to infinity. It does not have two axes of symmetry or like a circle. Hence, the given function is a parabola.
Now, let us see whether it passes through the origin. We know that at the origin x and y coordinates are 0. That is, the point $\left( 0,0 \right)$ . From the table, we can see that there exists a point in $y=2{{x}^{2}}$ .
Hence, $y=2{{x}^{2}}$ is a parabola passing through the origin.

So, the correct answer is “Option A”.

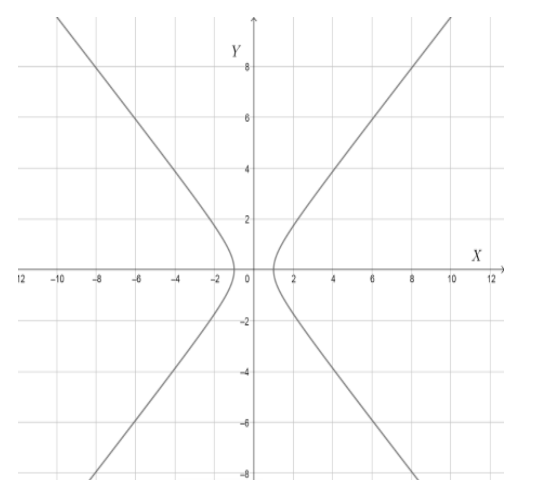
Note: Do not get confused with parabola and hyperbola. A hyperbola will have the equation of the form $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ . The graph of this will be like:

We can also solve this problem in an alternate way. If any equation is of the form shown below, then that function will be a parabola.
$y=a{{x}^{2}}+bx+c,\text{ }a\ne 0...(i)$
The given equation is $y=2{{x}^{2}}$
When we compare it with equation (i),
$a=2,b=0,c=0$
Hence, the given equation is of the form (i) and is a parabola.
Now to check whether it passes through origin, we can check the value of y for $x=0$ . That is
$y=2\times 0=0$
Hence, there exists a point $\left( 0,0 \right)$ for $y=2{{x}^{2}}$ . This means that $y=2{{x}^{2}}$ passes through the origin.
In other words, we can say that when either x or y is squared but not both, the given equation will be an equation of parabola.
When x and y are both squared and the coefficients are positive but different, then the given equation is the equation of ellipse.
When x and y are both squared, and exactly one of the coefficients is negative and exactly one of the coefficients is positive, then it resembles a hyperbola.