Question

What is the multiplicity of the real root of an equation that crosses/touches the $x$ axis once?

Answer 1

In this problem we need to check the multiplicity of the real root of an equation which crosses/touches the $x$ axis once. For this we will consider any two equations which touch or cross the $x$ axis once along with the roots of both the assumed equations. By observing the roots and graphs of the assumed equations we can simplify answering the question.

Complete step-by-step solution:
Let us assume the equation $f\left( x \right)={{x}^{3}}$.
The graph of the function $f\left( x \right)={{x}^{3}}$ would be

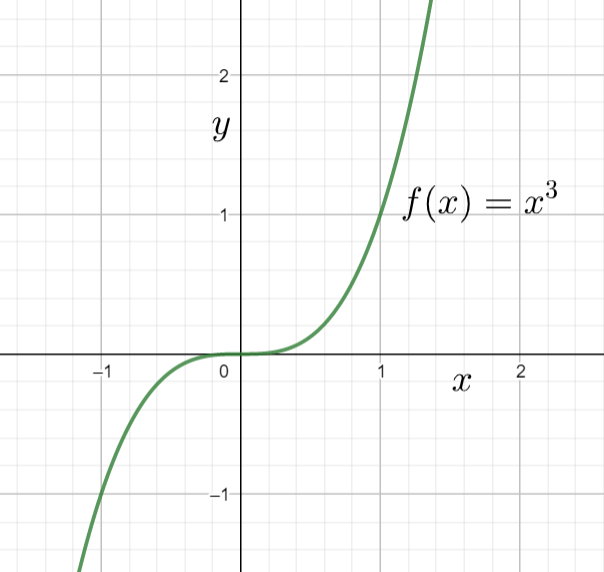
We can observe that the function $f\left( x \right)={{x}^{3}}$ touches the $x$ axis once. The roots of the equation $f\left( x \right)={{x}^{3}}$ are $x=0,0,0$. The multiplicity of the root $0$ is $3$.
Now let us consider the function $g\left( x \right)={{x}^{3}}+x$. The graph of the equation $g\left( x \right)={{x}^{3}}+x$ is given by

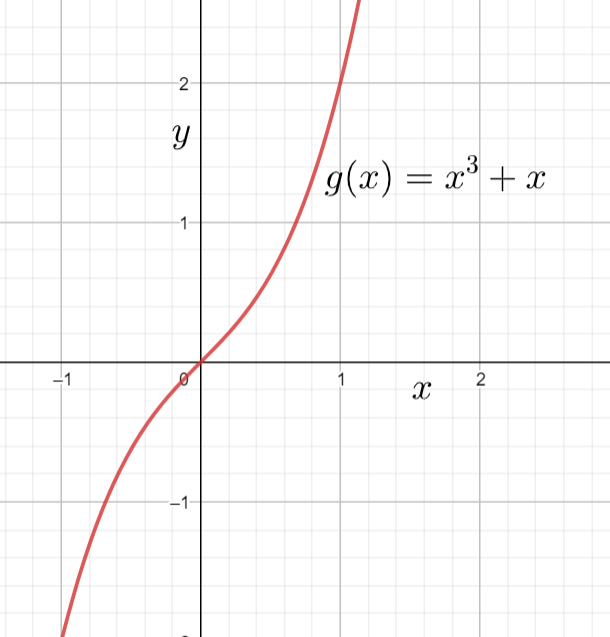
We can also observe that the equation $g\left( x \right)={{x}^{3}}+x$ touches the $x$ axis once. The real roots of the equation $g\left( x \right)={{x}^{3}}+x$ are $x=0$. The multiplicity of the root $0$ is $1$.
From the above two observations we can say that the multiplicity of a real root of an equation which touches the $x$ axis is independent of how many points the equation touches the $x$ axis.

Note: In this problem we have used the term multiplicity of the polynomial. We can define the multiplicity of a polynomial as the occurrence or appearance of a factor in the factorial form of the polynomial. It shows how the graph of the polynomial will look like.