Question

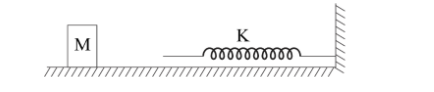
What is the momentum of the block before collision if the block having mass M is moving on the frictionless horizontal surface collides with a spring of constant K and compresses by L?

(A) $L\sqrt {MK}$
(B) $\dfrac{{K{L^2}}}{{2M}}$
(C) Zero
(D) $\dfrac{{M{L^2}}}{K}$

Answer 1

Hint Use the formula,
$K.E + P.E = E$
where, $K.E$ is the kinetic energy
$P.E$ is the potential energy
$E$ is the energy
Then, make use of the conservation of energy by making kinetic energy and potential energy equal to each other.

Step by Step Solution
We know that, if conservative forces acts on system only the mechanical energy remains constant
$\therefore K.E + P.E = E$(constant)
where, $K.E$ is the kinetic energy
$P.E$ is the potential energy
$E$ is the mechanical energy which is constant
$\Delta K + \Delta U = 0 \\\ \\\$
Therefore, $\Delta K = - \Delta U$
Let the initial velocity be $v$
then, kinetic energy is $\dfrac{1}{2}m{v^2}$
And final potential energy due to spring is $\dfrac{1}{2}k{x^2}$ (where, $x$is the compression)
According to conservation of energy, the energy inside a closed system remains constant
So, the kinetic energy becomes equal to the final potential energy
Therefore, $\dfrac{1}{2}M{v^2} = \dfrac{1}{2}K{x^2}$
$M{v^2} = K{x^2} \\\ {v^2} = \dfrac{{K{x^2}}}{M} \\\ v = x\sqrt {\dfrac{K}{M}} \\\$
Here, $x$is the compression. So, according to question $L =$compression
$\therefore v = L\sqrt {\dfrac{K}{M}} \cdots (1)$
Hence, maximum momentum, $P = Mv$
Using the value of $v$ from equation $(1)$ in the formula of momentum
$P = L\sqrt {MK}$

From above, we can say that option (A) is correct.

Note The mechanical energy remains constant when conservative forces act only on the system.
In the conservation of energy, we can say that the two energies become equal to each other because energy inside the closed system remains constant therefore, both become equal.
Momentum is the product of mass and velocity and is denoted by $P$ so, we can express momentum as:
$P = Mv$