Question: What is the moment of inertia of a ring about a tangent to the circle of the ring?...

Question

What is the moment of inertia of a ring about a tangent to the circle of the ring?

Answer 1

Solution

We first start with the definition of the moment of inertia. The moment of inertia also known as rotational inertia defined as a quantity that is equal to the sum of the product of the mass of every particle with its square of the distance from the rotation axis. After establishing the formula for the moment of inertia, we use the parallel axis theorem on it.

Complete answer:
As we know that the moment of inertia $I$ is defined as the sum of the product of the mass $M$ of the particles with its square of the distance $R$ from the rotational axis. Hence given as
$\Rightarrow I = M{R^2}$
Now for a circular ring, the moment of inertia about an axis of the rotation passing through the centre of the ring which lies in its plane is given as
$\Rightarrow {I_r} = \dfrac{{M{R^2}}}{2}$ ………. $(1)$

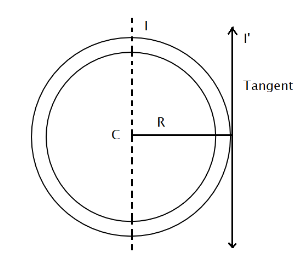
Now it is given in the question a tangent of the circle of the ring that touches one of its surfaces can be found to be parallel to the diameter of the ring. Here from the figure, we can see that the distance between the two parallel axes $R$ is also the radius of the ring. Hence from the parallel axis theorem, we can conclude that
$\Rightarrow {I_{T} } = {I_r} + M{R^2}$
Where ${I_r}$ is the moment of inertia of the ring about an axis passing through the centre and ${I_T}$ is the moment of inertia of tangent.
Hence substituting from the equation $(1)$ , the equation results in
$\Rightarrow {I_{T} } = \dfrac{{M{R^2}}}{2} + M{R^2}$
$\therefore {I_{T} } = \dfrac{{3M{R^2}}}{2}$
Therefore the moment of inertia of a ring about a tangent to the circle of the ring is ${I_{T} } = \dfrac{{3M{R^2}}}{2}$ .

Note:
Moment of inertia of a rigid body is a quantity that determines the torque needed for a required angular acceleration about a rotational axis. The moment of inertia can be calculated by using two methods: the first method is the parallel axis theorem and the other is the perpendicular theorem. In this question, we have used the parallel axis theorem.