Solveeit Logo
Login

Question

Question: What is the minimum value of \(F\) needed so that block begins to move upward on frictionless inclin...

What is the minimum value of FF needed so that block begins to move upward on frictionless incline plane as shown

Explanation

Solution

In the given question we have to find all the forces and the tension forces that work on the body MM. Thus, we have to formulate a free body diagram here. Then by using the trigonometric ratios and Newton’s Law we will find the force FF that is needed to move the block upwards.

Complete step by step answer:

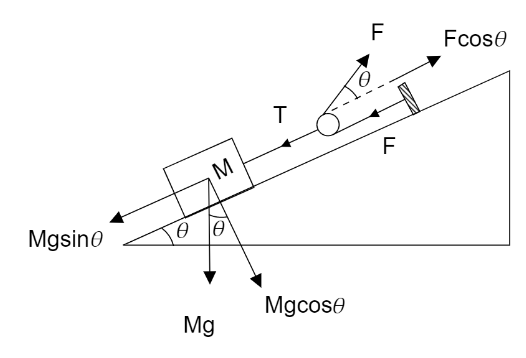
In the given figure, it is clear that the weight MgMg acts downward.By resolving the components of the weight MgMg we get the vertical component is Mgcos⁡θMg\cos \theta and the horizontal component is Mgsin⁡θMg\sin \theta . The horizontal component Mgsin⁡θMg\sin \theta is the force that balances the tension TT of the string.We can write,
T=Mgsin⁡θ−−−−−(1)T = Mg\sin \theta - - - - - \left( 1 \right)

Now, resolving the components of the force FF which is actually the tension in the string.
The horizontal component of the tension or force FF is Fcos⁡θF\cos \theta .Hence from the given diagram we get,
T=F+Fcos⁡θ−−−−−(2)T = F + F\cos \theta - - - - - \left( 2 \right)
Comparing both the equations it is clear that,
F+Fcos⁡θ=Mgsin⁡θF + F\cos \theta = Mg\sin \theta
Taking FF common from the left side of the equation we get,
F(1+cos⁡θ)=Mgsin⁡θF\left( {1 + \cos \theta } \right) = Mg\sin \theta

From the half angle formula of the trigonometry we get,
F(2cos⁡2θ2)=Mg(2sin⁡θ2cos⁡θ2)F\left( {2{{\cos }^2}\dfrac{\theta }{2}} \right) = Mg\left( {2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}} \right)
Dividing both sides by 2cos⁡θ22\cos \dfrac{\theta }{2} we get,
F(cos⁡θ2)=Mg(sin⁡θ2)F\left( {\cos \dfrac{\theta }{2}} \right) = Mg\left( {\sin \dfrac{\theta }{2}} \right)
Arranging the equation we get,
F=Mg(sin⁡θ2cos⁡θ2) ∴F=Mgtan⁡θ2F = Mg\left( {\dfrac{{\sin \dfrac{\theta }{2}}}{{\cos \dfrac{\theta }{2}}}} \right) \\\ \therefore F= Mg\tan \dfrac{\theta }{2}

So, the minimum value of force FF must be Mgtan⁡θ2Mg\tan \dfrac{\theta }{2} in order to move the block upward.

Note: It must be noted that the given question stated that the plane is frictionless. If there is friction on the surface, it will oppose the motion of the body. Thus, we have calculated a force in opposite direction to the force required to move the body upwards to find the equation of the forces that balances each other.