Question

What is the minimum value of $d$ for which final image and object are at the same place

A. $30\,cm$
B. $40\,cm$
C. $20\,cm$
D. $80\,cm$

Answer 1

In order to find the solution for the above question, we will examine the diagram given in the question and will note down all the information provided. We will then understand a small concept known as the principle of reversibility. Using this principle, we will determine the path to obtain our desired image. Finally, using the lens formulae, we will calculate and find our answer.

Formula used:
Lens Formula:
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$
Where $f$ is the focal length, $v$ is the image distance and $u$ is the object distance.

Complete step by step answer:
As we can see from the figure, we have a construction of a mirror and a lens separated by a distance. The lens is a convex lens and the mirror is a convex mirror. First of all, we will discuss the data given in the question above. The convex lens has a focal length of ${{F}_{L}}=20\,cm$. Therefore the center of curvature of this lens would be at a distance of ${{C}_{L}}=40\,cm$ from the pole of the lens.

Therefore, we can conclude that the object $Q$ is placed between the focal length and the center of curvature at a distance of $u=30\,cm$. The focal length of the convex mirror is given as ${{F}_{m}}=10cm$. Therefore, its center of curvature is at a distance of ${{C}_{m}}=20\,cm$ from the pole of the mirror. In the construction, both the mirror and the lens are separated by a distance of $d$from each other.

Now, given all the information we mentioned above, it is asked that what is the separation between the lens and the mirror if the image is obtained at the same point as of the object and is of the same size as that of the object. The best way to obtain an image at the same position as that of the object is to use the principle of reversibility.

The theory of reversibility of light states that if the direction of light movement is reversed, it will follow the same course. The theory of reversibility states that the attenuation of a light ray caused by reflection, refraction, and absorption during its passage through an optical medium is unaffected by reversing the ray's direction. The theory of reversibility is a derivation of Snell's law of light refraction in its most basic form. The theory of reversibility states that the attenuation of a light ray caused by reflection, refraction, and absorption during its passage through an optical medium is unaffected by reversing the ray's direction.

Using the theory of principle of reversibility, we can interpret that the simplest way to obtain the image at the same position as that of the image is by reversing the ray of lights coming from the object.

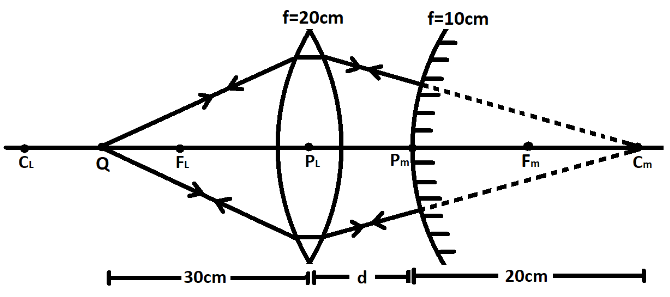
As we can see from the above figure, the rays emerging from the object travel to the lens. Falling on the lens, the rays undergo refraction due to the refractive index of the lens. After getting refracted on both the surfaces of the lens, the rays strike the mirror which is placed at a distance $d$from the mirror. As we want the rays to get reversed, we suppose that the rays strike perpendicular to the surface of the mirror and travel back on its initial path. If these rays are traced back behind the mirror, they meet at the center of curvature of the mirror. The rays undergo a refraction again and form an image at the same position as that of the object.

We want to find the distance of separation between the lens and the mirror. As we know that the image formed by the convex lens will be at the center of curvature of the convex mirror. Hence, using the mirror formula:
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u} \\\ \Rightarrow \dfrac{1}{{{F}_{L}}}=\dfrac{1}{d+{{C}_{m}}}+\dfrac{1}{u} \\\$
As the image is formed at the center of curvature of the mirror, the image distance from the lens$v=d+{{C}_{m}}$. As the object distance is measured in negative on the left side of the lens $u=-u$.
\dfrac{1}{20}=\dfrac{1}{d+20}+\dfrac{1}{30} \\\ \Rightarrow \dfrac{1}{d+20}=\dfrac{1}{20}-\dfrac{1}{30} \\\ \Rightarrow \dfrac{1}{d+20}=\dfrac{30-20}{600} \\\ \Rightarrow \dfrac{1}{d+20}=\dfrac{1}{60} \\\ \Rightarrow d+20=60 \\\ \Rightarrow d=60-20 \\\ \therefore d=40\,cm \\\
Therefore, the separation of the lens and the mirror is $d=40cm$. Hence, the correct answer to our question is option B.

Note: It is very important to note that to obtain the image as the same size as that of the object and also at the same position as that of the object, the object needs to be placed at the center of curvature of the mirror. In this case, there is a lens in between the mirror and the object and hence, we need to consider the refraction of the rays which is caused at the surfaces of the lens.