Question

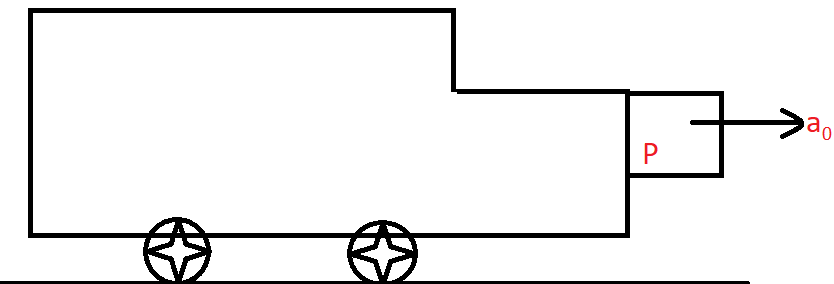
What is the minimum ${\text{acceleration (}}{{\text{a}}_0})$ of the cart in the given figure so that block P will not fall? (Assume coefficient of friction $\mu$ ).

A. $\dfrac{g}{{\sqrt \mu }}$
B. $\dfrac{g}{\mu }$
C. $2\mu g$
D. ${\mu ^2}g$

Answer 1

Friction force is the resistant force or opposing force which generates when surfaces slide making contact with each other. When in contact friction force is multiple of coefficient of friction with normal force. Normal force is the force on an object that acts perpendicularly with the contact surface. In this also we need to specify the value of normal force.

Complete step by step solution:
Assume the mass of the block P is $m$ . Block P will experience a downward force $mg$ due to its weight which will make the block fall down sliding the surface of the cart.
$mg$ = weight of body …………..(downward)
As our cart is in accelerated motion hence, it will apply a force on the block P which will be due to acceleration it produces in body P i.e. the net resultant acceleration which is ${a_0}$ . So the force to be applied due to acceleration in the cart will be product of mass of block with resultant acceleration i.e.
$m{a_0}$ = Force on block P by accelerated cart ………………(in direction of motion of cart)
If we look at carefully we will notice that block is suspended with cart by making a contact and the point where contact is made, there act a force perpendicular to surface opposite to other perpendicular force with surface i.e.
$N$ = Normal Force ………..(opposite to force applied by cart as that is only perpendicular force with surface of block P)
Now as the block makes contact with the cart hence any force that causes a sliding effect will generate friction. In direction of motion there is no point for the block to make motion with sliding. In a vertical plane the body can move with sliding hence friction force will generate in direction opposite to weight until the body is in a static condition. On losing static condition friction force also changes direction.
$f$ = Frictional Force
To keep the block P in rest it is mandatory that all forces balance each other. As the block is in rest hence it will face static friction in direction opposite to weight.
Draw a free body diagram to show all kinds of forces acting on the body.

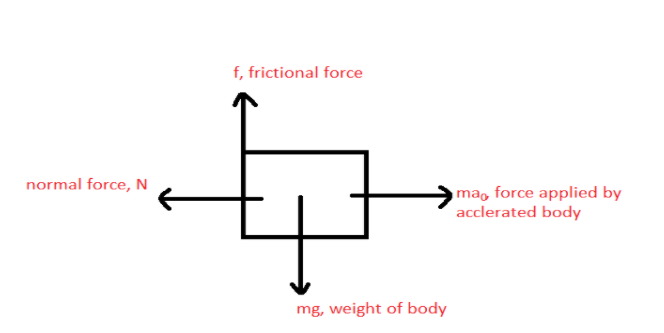
Balancing all forces we get,
$mg = f$ ……………(i)
$m{a_0} = N$ ………….(ii)
According to question, Coefficient of friction of block is $\mu$
Frictional force acting will be,
$f = \mu \times N\,\,......\,({\text{iii)}}$
Putting value of normal force from equation $({\text{ii)}}$ in equation $({\text{iii)}}$ ,
$f = \mu \times m{a_0}$
Putting obtained value of frictional force in equation $({\text{i)}}$ ,
$mg = \mu m{a_0}$
Evaluating the equation we get,
${a_0} = \dfrac{g}{\mu }$
The acceleration of the cart to prevent the block from falling is $\dfrac{g}{\mu }$ .

Note:
One must never forget that normal always acts perpendicular to surface of contact and frictional force is its multiple with coefficient of friction. Drawing free body diagrams provide an insight into the point and direction of action of forces and in cases of balancing forces it provides a good overview and accuracy.